
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:填空题
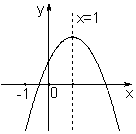 二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;
二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {4,6} | B. | {1,4,6} | C. | ∅ | D. | {2,3,4,5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在△ABC中,若sinA>sinB,则A>B | B. | 在△ABC中,若A≤B,则sinA≤sinB | ||
| C. | 在△ABC中,若sinA<sinB,则A<B | D. | 在△ABC中,若sinA≤sinB,则A≤B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{15}}{15}$ | B. | $\frac{\sqrt{15}}{15}$ | C. | $\frac{2\sqrt{15}}{15}$ | D. | $\frac{\sqrt{15}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
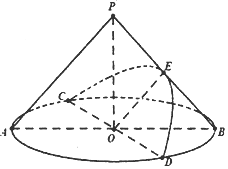 如图,在底面半径和高均为4的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,若过直径CD与点E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为$\sqrt{10}$.
如图,在底面半径和高均为4的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,若过直径CD与点E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为$\sqrt{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11,3 | B. | 3,11 | C. | 3,80 | D. | 80,3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com