Question

7．在棱长为a的正方体ABCD-A₁B₁C₁D₁中，M是AB的中点，则点C到平面A₁DM的距离为$\frac{\sqrt{6}}{3}$a．

Answer 1

分析 连接A₁C、MC，三棱锥A₁-DMC就是三棱锥C-A₁MD，利用三棱锥的体积公式进行转换，即可求出点C到平面A₁DM的距离．

解答 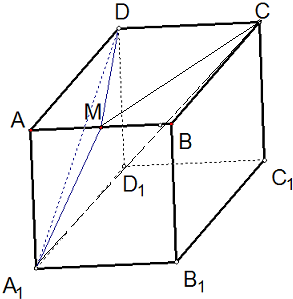解：连接A₁C、MC可得：
S_△CMD=$\frac{1}{2}$S _ABCD=$\frac{1}{2}$a²，
△A₁DM中，A₁D=$\sqrt{2}$a，A₁M=MD=$\frac{\sqrt{5}}{2}$a，
∴S_△A1MD=$\frac{1}{2}$A₁M•MDsinA ₁MD=$\frac{\sqrt{6}}{4}$a，
三棱锥的体积：V _A1-MCD=V _C-A1DM
所以 $\frac{1}{3}$S_△MCD×AA₁=$\frac{1}{3}$S_△AD1M×d  （设d是点C到平面A₁DM的距离），
∴d=$\frac{\sqrt{6}}{3}$a．
故答案为$\frac{\sqrt{6}}{3}$a．

点评 本题以正方体为载体，考查了立体几何中点、线、面的距离的计算，属于中档题．运用体积计算公式，进行等体积转换来求点到平面的距离，是解决本题的关键．