
【题目】一动圆与圆![]() 外切,与圆
外切,与圆![]() 内切.
内切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)设过圆心![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 相交于
相交于![]() 两点,
两点,![]() (
(![]() 为圆
为圆![]() 的圆心)的内切圆
的圆心)的内切圆![]() 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)利用动圆与圆![]() 外切,与圆
外切,与圆![]() 内切,可得
内切,可得![]()
![]() ,由椭圆定义知
,由椭圆定义知![]() 是以
是以![]() 为焦点的椭圆,从而可得动圆圆心
为焦点的椭圆,从而可得动圆圆心![]() 的轨迹
的轨迹![]() 的方程;(2)当
的方程;(2)当![]() 最大时,
最大时,![]() 也最大,
也最大,![]() 内切圆的面积也最大,表示出三角形的面积,利用换元法,结合导数,可求得最值.
内切圆的面积也最大,表示出三角形的面积,利用换元法,结合导数,可求得最值.
试题解析:(1)设动圆圆心为![]() ,半径为
,半径为![]() ,即可求得结论.
,即可求得结论.
由题意,动圆与圆![]() 外切,与圆
外切,与圆![]() 内切,
内切,![]() ,由椭圆定义知
,由椭圆定义知![]() 在
在![]() 为焦点的椭圆上,且
为焦点的椭圆上,且![]() ,
,![]() ,
,![]() 动圆圆心
动圆圆心![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
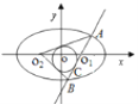
(2)如图,设![]() 内切圆
内切圆![]() 的半径为
的半径为![]() ,与直线
,与直线![]() 的切点为
的切点为![]() ,则三角形
,则三角形![]() 的面积
的面积![]()
![]() ,当
,当![]() 最大时,
最大时,![]() 也最大,
也最大,![]() 内切圆的面积也最大,设
内切圆的面积也最大,设![]() ,则
,则
![]() ,由
,由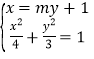 ,得
,得![]() ,解得
,解得![]() ,
,![]() ,令
,令![]() ,则
,则![]() ,且
,且![]() ,有
,有![]() ,令
,令![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上单调递增,有
上单调递增,有![]() ,
,![]() ,即当
,即当![]() 时,
时,![]() 有最大值
有最大值![]() ,得
,得![]() ,这时所求内切圆的面积为
,这时所求内切圆的面积为![]() 存在直线
存在直线![]() ,
,![]() 的内切圆
的内切圆![]() 的面积最大值为
的面积最大值为![]() .
.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求函数y=f(x)的解析式,并用“五点法作图”在给出的直角坐标系中画出函数y=f(x)在区间[0,π]上的图象; 
(2)设α∈(0,π),f( ![]() )=
)= ![]() ,求sinα的值.
,求sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( ) 
A.31.2
B.32.4
C.33.6
D.34.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《最强大脑》是江苏卫视推出国内首档大型科学类真人秀电视节目,该节目集结了国内外最顶尖的脑力高手,堪称脑力界的奥林匹克,某校为了增强学生的记忆力和辨识力也组织了一场类似《最强大脑》的PK赛,A、B两队各由4名选手组成,每局两队各派一名选手PK,除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分,假设每局比赛两队选手获胜的概率均为0.5,且各局比赛结果相互独立.
(1)求比赛结束时A队的得分高于B队的得分的概率;
(2)求比赛结束时B队得分X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,设倾斜角为
中,设倾斜角为![]() 的直线
的直线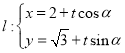 (
(![]() 为参数)与曲线
为参数)与曲线![]() (
(![]() 为参数)相交于不同的两点
为参数)相交于不同的两点![]() .
.
(1)若![]() ,求线段
,求线段![]() 中点
中点![]() 的坐标;
的坐标;
(2)若![]() ,其中
,其中![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”;若
的“不动点”;若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”.函数
的“稳定点”.函数![]() 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,
,![]() .
.
(![]() )设函数
)设函数![]() ,求集合
,求集合![]() 和
和![]() .
.
(![]() )求证:
)求证:![]() .
.
(![]() )设函数
)设函数![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的值域;
的值域;
(2)当![]() 时,函数
时,函数![]() 的图象关于
的图象关于![]() 对称,求函数
对称,求函数![]() 的对称轴.
的对称轴.
(3)若![]() 图象上有一个最低点
图象上有一个最低点![]() ,如果图象上每点纵坐标不变,横坐标缩短到原来的
,如果图象上每点纵坐标不变,横坐标缩短到原来的![]() 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得![]() 的图象,又知
的图象,又知![]() 的所有正根从小到大依次为
的所有正根从小到大依次为![]() ,且
,且![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定直线![]() ,抛物线
,抛物线![]() ,且抛物线
,且抛物线![]() 的焦点在直线
的焦点在直线![]() 上.
上.
(1)求抛物线![]() 的方程
的方程
(2)若![]() 的三个顶点都在抛物线
的三个顶点都在抛物线![]() 上,且点
上,且点![]() 的纵坐标
的纵坐标![]() ,
, ![]() 的重心恰是抛物线
的重心恰是抛物线![]() 的焦点
的焦点![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com