
����Ŀ������ǿ���ԡ��ǽ��������Ƴ����������Ϳ�ѧ����������ӽ�Ŀ���ý�Ŀ�����˹����������������֣�����������İ���ƥ�ˣ�ijУΪ����ǿѧ���ļ������ͱ�ʶ��Ҳ��֯��һ�����ơ���ǿ���ԡ���PK����A��B���Ӹ���4��ѡ����ɣ�ÿ�����Ӹ���һ��ѡ��PK����������ʤ�ߵ�2���⣬�������ʤ�߾���1�֣�ÿ�ֵĸ��ߵ�0�֣�����ÿ�ֱ�������ѡ�ֻ�ʤ�ĸ��ʾ�Ϊ0.5���Ҹ��ֱ�������������
��1�����������ʱA�ӵĵ÷ָ���B�ӵĵ÷ֵĸ��ʣ�
��2�����������ʱB�ӵ÷�X�ķֲ��к�������
���𰸡�
��1���⣺���¼�����������ʱA�ӵĵ÷ָ���B�ӵĵ÷֡�ΪA���¼�����������ʱB�ӵĵ÷ָ���a�ӵĵ÷֡����¼�����������ʱA�ӵĵ÷ֵ���B�ӵĵ÷֡�Ϊ�¼�C�����ݣ�ÿ�ֱ�������ѡ�ֻ�ʤ�ĸ��ʾ�Ϊ0.5��
��P��A��=P��B����P��A��+P��B��+P��C��=1��P��C��=0��
��P��A��= ![]()
��2���⣺X�Ŀ���ȡֵΪ0��1��2��3��4��5��
P��X=0��= ![]() =
= ![]() ��P��X=1��=
��P��X=1��= ![]() =
= ![]() ��
��
P��X=2��= ![]() +
+ ![]() =
= ![]() ��
��
P��X=3��= ![]() +
+ ![]() ��
�� ![]() =
= ![]() ��
��
P��X=4��= ![]() =
= ![]() ��P��X=5��=
��P��X=5��= ![]() =
= ![]() ��
��
X | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
E��X��=0�� ![]() +1��
+1�� ![]() +2��
+2�� ![]() +3��
+3�� ![]() +4��
+4�� ![]() +5��
+5�� ![]() =
= ![]()
����������1�����¼�����������ʱA�ӵĵ÷ָ���B�ӵĵ÷֡�ΪA���¼�����������ʱB�ӵĵ÷ָ���a�ӵĵ÷֡����¼�����������ʱA�ӵĵ÷ֵ���B�ӵĵ÷֡�Ϊ�¼�C�����ݣ�ÿ�ֱ�������ѡ�ֻ�ʤ�ĸ��ʾ�Ϊ0.5���ɵ�P��A��=P��B����P��A��+P��B��+P��C��=1��P��C��=0�����ɵó�P��A������2��X�Ŀ���ȡֵΪ0��1��2��3��4��5������������뻥���¼��ĸ��ʼ��㹫ʽ���ɵó���


 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����ABCDΪ�����Σ�PA�͵���ABCD��AD=AP��EΪ��PD�е㣮 
��1����֤��PD��ƽ��ABE��
��2����FΪAB�е㣬 ![]() ����ȷ���˵�ֵ��ʹ�����P��FM��B������ֵΪ
����ȷ���˵�ֵ��ʹ�����P��FM��B������ֵΪ ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ����Բ
����Բ![]() ��
��![]() �Ķ���λ��
�Ķ���λ��![]() ���·��Ķ˵㣬��
���·��Ķ˵㣬��![]() ��б��Ϊ1��ֱ�߽���Բ��
��б��Ϊ1��ֱ�߽���Բ��![]() �㣬��
�㣬��![]() ��
��![]() ���ϣ���
���ϣ���![]() �ᣬ
�ᣬ ![]() ��
��
��1������![]() ������Ϊ
������Ϊ![]() ������Բ
������Բ![]() �ķ��̣�
�ķ��̣�
��2������![]() ������Ϊ
������Ϊ![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ȳ�����{an}�Ĺ���d��0��ǰn���ΪSn �� ��֪3 ![]() �ǩ�a2��a9�ĵȱ����S10=��20��
�ǩ�a2��a9�ĵȱ����S10=��20��
��1��������{an}��ͨ�ʽ��
��2����bn= ![]() ��������{bn}��ǰn���Tn��n��6����
��������{bn}��ǰn���Tn��n��6����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ȡij��ѧ�ס��������10��ͬѧ���������ǵ����ߣ���λ��cm��������������ݵľ�Ҷͼ��ͼ7.

��1�����ݾ�Ҷͼ�ж��ĸ����ƽ�����߽ϸߣ�
��2������װ���������
��3���ִ��Ұ���10��ͬѧ�������ȡ�������߲�����173cm��ͬѧ��������Ϊ176cm��ͬѧ�����еĸ��ʡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ijѧУ�����꼶��800�������������ȡ50���������ߣ��������ֱ���ѧ������ȫ������155cm��195cm֮�䣬��������������·�ʽ�ֳɰ��飺��һ��[155,160)���ڶ���[160,165)�������ڰ���[190,195]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪��һ����ڰ���������ͬ�������顢�����顢�ڰ����������ι��ɵȲ����У�
��1����������ѧУ�����꼶ȫ����������180cm����(��180cm)��������
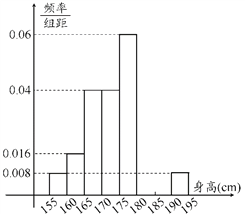
��2��������顢�������Ƶ�ʲ���������Ƶ�ʷֲ�ֱ��ͼ���������ӿ̶����������ϱ�dz����ݣ�����ֱ����ͼ����
��3����ֱ��ͼ�����������ߵ���λ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��Բ��Բ![]() ���У���Բ
���У���Բ![]() ���У�
����
��1����ԲԲ��![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�
�ķ��̣�
��2�����Բ��![]() ��ֱ��
��ֱ��![]() ��켣
��켣![]() �ཻ��
�ཻ��![]() ���㣬
���㣬![]() ��
��![]() ΪԲ
ΪԲ![]() ��Բ�ģ�������Բ
��Բ�ģ�������Բ![]() ������Ƿ�������ֵ�������ڣ����������ֵ��ֱ��
������Ƿ�������ֵ�������ڣ����������ֵ��ֱ��![]() �ķ��̣��������ڣ���˵�����ɣ�
�ķ��̣��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �Ƿ���
�Ƿ���![]() ������, ����
������, ����![]() �ǹ���Ϊ���ĵȲ����У�����
�ǹ���Ϊ���ĵȲ����У�����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ,��
,��![]() .
.
(1)������![]() ��ͨ�ʽ��
��ͨ�ʽ��
(2)��![]() ,������
,������![]() ��ǰ
��ǰ![]() ���
���![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ���ı���ABCD�У�AB= ![]() ��BC=2��AC��CD��AC=CD�����ı���ABCD��������ֵΪ ��
��BC=2��AC��CD��AC=CD�����ı���ABCD��������ֵΪ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com