Question

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，PA⊥底面ABCD，AD=AP，E为棱PD中点．
（1）求证：PD⊥平面ABE；
（2）若F为AB中点， ，试确定λ的值，使二面角P﹣FM﹣B的余弦值为 ．

Answer 1

【答案】
（1）证明：∵PA⊥底面ABCD，AB底面ABCD，∴PA⊥AB，

又∵底面ABCD为矩形，∴AB⊥AD，PA∩AD=A，PA平面PAD，AD平面PAD，

∴AB⊥平面PAD，又PD平面PAD，∴AB⊥PD，AD=AP，E为PD中点，∴AE⊥PD，AE∩AB=A，AE平面ABE，AB平面ABE，∴PD⊥平面ABE

（2）解：以A为原点，以 为x，y，z轴正方向，建立空间直角坐标系A﹣BDP，令|AB|=2，

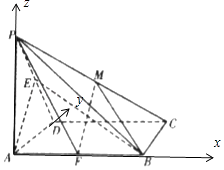
则A（0，0，0），B（2，0，0），P（0，0，2），C（2，2，0），E（0，1，1），F（1，0，0）， ， ， ，M（2λ，2λ，2﹣2λ）

设平面PFM的法向量 ， ，即 ，

设平面BFM的法向量 ， ，

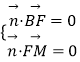即 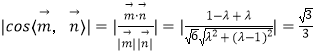， ，解得

【解析】（I）证明AB⊥平面PAD，推出AB⊥PD，AE⊥PD，AE∩AB=A，即可证明PD⊥平面ABE．（II） 以A为原点，以 为x，y，z轴正方向，建立空间直角坐标系A﹣BDP，求出相关点的坐标，平面PFM的法向量，平面BFM的法向量，利用空间向量的数量积求解即可．