
【题目】在直三棱柱![]() 中,
中, ![]() ,∠ACB=90°,M是
,∠ACB=90°,M是![]() 的中点,N是
的中点,N是![]() 的中点.
的中点.
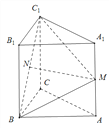
(Ⅰ)求证:MN∥平面![]() ;
;
(Ⅱ)求点![]() 到平面BMC的距离.
到平面BMC的距离.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)根据图形取B1C1中点D,连结ND、A1D,得到四边形A1MND为平行四边形,从而得到线面平行。(2)先证得BC⊥平面A1MC1,过C1作C1H⊥CM,又BC⊥C1H,故C1H为C1点到平面BMC的距离,从而得到点面距离。
解析:
(1)如图所示,取B1C1中点D,连结ND、A1D ∴DN∥BB1∥AA1
又DN=![]() ,∴四边形A1MND为平行四边形。
,∴四边形A1MND为平行四边形。
∴MN∥A1 D 又MN ![]() 平面A1B1C1,AD1
平面A1B1C1,AD1![]() 平面A1B1C1 ∴MN∥平面
平面A1B1C1 ∴MN∥平面![]()
(2)因三棱柱![]() 为直三棱柱, ∴C1 C ⊥BC,又∠ACB=90°∴BC⊥平面A1MC1
为直三棱柱, ∴C1 C ⊥BC,又∠ACB=90°∴BC⊥平面A1MC1
在平面ACC1 A1中,过C1作C1H⊥CM,又BC⊥C1H,故C1H为C1点到平面BMC的距离。
在等腰三角形CMC1中,C1 C=2![]() ,CM=C1M=
,CM=C1M=![]() ∴.
∴. ![]() 。
。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(2ax+1)+ ![]() ﹣2ax(a∈R).
﹣2ax(a∈R).
(1)若x=2为f(x)的极值点,求实数a的值;
(2)若y=f(x)在[3,+∞)上为增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点. 
(1)求证:PD⊥平面ABE;
(2)若F为AB中点, ![]() ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为
,试确定λ的值,使二面角P﹣FM﹣B的余弦值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,周期是
,周期是![]() .
.
(1)求函数解析式,并写出函数图象的对称轴方程和对称中心;
(2)已知点![]() ,点
,点![]() 是该函数图象上一点,点
是该函数图象上一点,点![]() 是
是![]() 的中点,当
的中点,当![]() ,
, ![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的顶点与焦点分别是椭圆![]() 的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 表示三条不同的直线,
表示三条不同的直线,![]() 表示三个不同的平面,给出下列四个命题:
表示三个不同的平面,给出下列四个命题:
①若![]() ,则
,则![]() ;
;
②若![]()
![]() ,则
,则![]() ;
;
③若![]() 为异面直线,
为异面直线,![]() ,
,![]() ,则
,则![]() ;
;
④若![]() ,则
,则![]() . 其中真命题的个数为( )
. 其中真命题的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50名测量身高,测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165)、…、第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(1)估计这所学校高三年级全体男生身高180cm以上(含180cm)的人数;
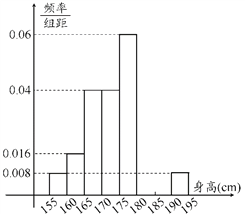
(2)求第六组、第七组的频率并补充完整频率分布直方图(如需增加刻度请在纵轴上标记出数据,并用直尺作图);
(3)由直方图估计男生身高的中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com