
【题目】如图,直三棱柱 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上的动点.
上的动点.
证明: ![]() ;
;
若平面![]() 分该棱柱为体积相等的两个部分,试确定点
分该棱柱为体积相等的两个部分,试确定点![]() 的位置,并求二面角
的位置,并求二面角![]() 的大小.
的大小.
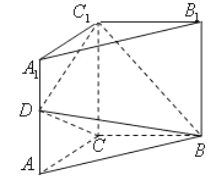
【答案】(1)见解析(2)30°
【解析】试题分析:(1)由![]() 平面
平面![]() 得
得![]() ,再由
,再由![]() ,得
,得![]() 平面
平面![]() ,
,
所以![]() ;(2)根据割补法求
;(2)根据割补法求![]() ,根据体积为三棱柱一半,求得
,根据体积为三棱柱一半,求得![]() 为
为![]() 中点;)取
中点;)取![]() 的中点
的中点![]() ,根据垂直关系可得
,根据垂直关系可得![]() 是二面角
是二面角![]() 的平面角.最后解三角形可得二面角
的平面角.最后解三角形可得二面角![]() 的大小
的大小
试题解析:解:(I)![]() 平面
平面![]() ,
, ![]()
又![]() ,即
,即![]()
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
, ![]() ;
;
(II) ![]() ,
,
依题意![]() ,
,
![]() 为
为![]() 中点;
中点;
(法1)取![]() 的中点
的中点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]()
![]() ,面
,面![]() 面
面![]() 面
面![]()
![]() ,得点
,得点![]() 与点
与点![]() 重合,且
重合,且![]() 是二面角
是二面角![]() 的平面角.
的平面角.
设![]() ,则
,则![]() ,得二面角的大小为30°.
,得二面角的大小为30°.
(法2)以![]() 为空间坐标原点,
为空间坐标原点, ![]() 为
为![]() 轴正向、
轴正向、![]() 为
为![]() 轴正向、
轴正向、![]() 为
为![]() 轴正向,建立空间直角坐标系,设
轴正向,建立空间直角坐标系,设![]() 的长为 1,则
的长为 1,则![]() .
.
作![]() 中点
中点![]() ,连结
,连结![]() ,则
,则![]() ,从而
,从而![]() 平面
平面![]() ,平面
,平面![]() 的一个法向量
的一个法向量![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则![]()
 ,令
,令![]() ,得
,得![]() ,
, ![]()
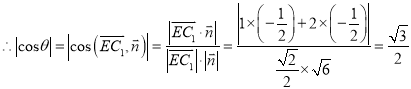
故二面角![]() 为30°.
为30°.


科目:高中数学 来源: 题型:
【题目】(本小题满分![]() 分)
分)
已知半径为![]() 的圆的圆心在
的圆的圆心在![]() 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线![]() 相切.
相切.
(Ⅰ)求圆的方程.
(Ⅱ)设直线![]() 与圆相交于
与圆相交于![]() ,
, ![]() 两点,求实数
两点,求实数![]() 的取值范围.
的取值范围.
(Ⅲ)在(Ⅱ)的条件下,是否存在实数![]() ,使得点
,使得点![]() 到
到![]() ,
, ![]() 两点的距离相等,若存在,求出实数
两点的距离相等,若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|,不等式f(x)≤3的解集为[﹣1,5].
(Ⅰ)求实数a的值;
(Ⅱ)若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】父亲节小明给爸爸从网上购买了一双运动鞋,就在父亲节的当天,快递公司给小明打电话话说鞋子已经到达快递公司了,马上可以送到小明家,到达时间为晚上6点到7点之间,小明的爸爸晚上5点下班之后需要坐公共汽车回家,到家的时间在晚上5点半到6点半之间。求小明的爸爸到家之后就能收到鞋子的概率(快递员把鞋子送到小明家的时候,会把鞋子放在小明家门口的“丰巢”中)为 __________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,![]() ,
,![]() ,F分别在线段BC和AD上,
,F分别在线段BC和AD上,![]() ,将矩形ABEF沿EF折起
,将矩形ABEF沿EF折起![]() 记折起后的矩形为MNEF,且平面
记折起后的矩形为MNEF,且平面![]() 平面ECDF.
平面ECDF.

![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面MFD;
平面MFD;
![]() Ⅱ
Ⅱ![]() 若
若![]() ,求证:
,求证:![]() ;
;
![]() Ⅲ
Ⅲ![]() 求四面体NFEC体积的最大值.
求四面体NFEC体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点. 
(1)求证:PD⊥平面ABE;
(2)若F为AB中点, ![]() ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为
,试确定λ的值,使二面角P﹣FM﹣B的余弦值为 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com