练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某市为了制定合理的节水方案，对居民用水情况进行了调查，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5），[0.5,1），[4,4.5]分成9组，制成了如图所示的频率分布直方图.

    （I）求直方图中的a值；

    （II）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，说明理由。

    【答案】（I）a=0.3；（II）3.6万

    【解析】试题分析：（1）有频率之和等于 ；（2）夏秋频率

    万.

    试题解析：

    （I）∵1=（0.08+0.16+a+0.42+0.50+a+0.12+0.08+0.04）×0.5 …………3分

    整理可得：2=1.4+2a，

    ∴解得：a=0.3 ……………5分

    （II）估计全市居民中月均用水量不低于3吨的人数为3.6万，理由如下：

    由已知中的频率分布直方图可得月均用水量不低于3吨的频率为

    （0.12+0.08+0.04）×0.5=0.12， ……………8分

    又样本容量为30万，

    则样本中月均用水量不低于3吨的户数为30×0.12=3.6万． ……………10分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在以为顶点的五面体中，O为AB的中点，

    平面， ∥， ， ， ．

    （1）在图中过点O作平面，使得∥平面，并说明理由；

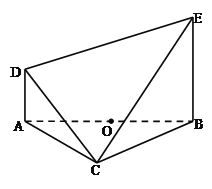
    （2）求直线DE与平面CBE所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{}的前n项和 (n为正整数)。

    （1）令，求证数列{}是等差数列，并求数列{}的通项公式；

    （2）令，试比较与的大小，并予以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在四棱柱，侧棱底面， ， ，且， ， ，侧棱.

    （1）若为上一点，试确定点的位置，使平面；

    （2）在（1）的条件下，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的最小正周期为.

    （1）求函数的单调增区间；

    （2）将函数的图象向左平移个单位，再向上平移1个单位，得到函数的图象，若在上至少含有10个零点，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， .

    （1）求函数在点点处的切线方程；

    （2）当时，求函数的极值点和极值；

    （3）当时， 恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知|a|＝4，|b|＝8，a与b的夹角是120°.

    (1) 计算：① |a＋b|，② |4a－2b|；


    (2) 当k为何值时，(a＋2b)⊥(ka－b)?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，矩形垂直于正方形垂直于平面．且．

    （1）证明：面面；

    （2）求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设各项均为正数的数列的前n项和为，满足，且，公比大于1的等比数列满足， .

    （1）求证数列是等差数列，并求其通项公式；

    （2）若，求数列的前n项和；

    （3）在（2）的条件下，若对一切正整数n恒成立，求实数t的取值范围.

    查看答案和解析>>

    同步练习册答案