
分析 用二倍角公式化简f(x),将|MN|表示成a的三角函数,
再化为正弦型函数,利用三角函数的有界性求出最大值.
解答 解:函数f(x)=2sin2x=1-cos2x,
函数$g(x)=\sqrt{3}sin2x$;
∴f(x)-g(x)=1-cos2x-$\sqrt{3}$sin2x
=-2($\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x)+1
=-2sin(2x+$\frac{π}{6}$)+1;
若直线x=a与函数f(x)和g(x)的图象分别交于M、N两点,
则|MN|=|f(a)-g(a)|=|-2sin(2a+$\frac{π}{6}$)+1|≤|2+1|=3,
∴|MN|的最大值为3.
故答案为:3.
点评 本题考查了三角函数的二倍角公式、诱导公式以及三角恒等变换和正弦函数的有界性问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
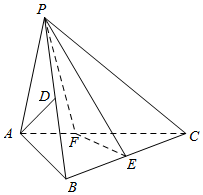 如图,在三棱锥P-ABC中,已知PA=AB,∠ABC为直角,PA⊥BC.点D,E分别为PB,BC的中点.
如图,在三棱锥P-ABC中,已知PA=AB,∠ABC为直角,PA⊥BC.点D,E分别为PB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数$f(x)=3sin({\frac{x}{2}+\frac{π}{6}})+3$
已知函数$f(x)=3sin({\frac{x}{2}+\frac{π}{6}})+3$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∨(¬q)是假命题 | D. | 命题p∧(¬q)是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com