设函数f(x)=xex,g(x)=ax2+x
(I)若f(x)与g(x)具有完全相同的单调区间,求a的值;
(Ⅱ)若当x≥0时恒有f(x)≥g(x),求a的取值范围.
解:(I)∵f(x)=xe
x,∴f′(x)=e
x+xe
x=(1+x)e
x,…(2分)
当x<-1时,f′(x)<0,∴f(x)在(-∞,-1)内单调递减;
当x>-1时,f′(x)>0,∴f(x)在(-1,+∞)内单调递增…(4分)
又g′(x)=2ax+1,由g′(-1)=-2a+1=0,得a=

,
此时g(x)=

x
2+x=

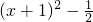
,
显然g(x)在(-∞,-1)内单调递减,在(-1,+∞)内单调递增,故a=

.…(6分)
(II)当x≥0时恒有f(x)≥g(x),即f(x)-g(x)=x(e
x-ax-1)≥0恒成立.…(7分)
故只需F(x)=e
x-ax-1≥0恒成立,
对F(x)求导数可得F′(x)=e
x-a.…(8分)
∵x≥0,∴F′(x)=e
x-a,
若a≤1,则当x∈(0,+∞)时,F′(x)>0,F(x)为增函数,
从而当x≥0时,F(x)≥F(0)=0,即f(x)≥g(x);…(10分)
若a>1,则当x∈(0,lna)时,F′(x)<0,F(x)为减函数,
从而当x∈(0,lna)时,F(x)<F(0)=0,即f(x)<g(x),故f(x)≥g(x)不恒成立.
故a的取值范围为:a≤1----(12分)
分析:(I)求f(x)的导数,可得单调区间,由极值点可得a值,可验证符合题意;
(Ⅱ)可转化为f(x)-g(x)=x(e
x-ax-1)≥0恒成立,令F(x)=e
x-ax-1,可得导数F′(x)=e
x-a,对a进行分类讨论可得结论.
点评:本题考查函数和导数的综合应用,涉及恒成立问题和分类讨论的思想,属中档题.

 ,
, x2+x=
x2+x=
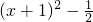 ,
, .…(6分)
.…(6分)
