
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,点
,点![]() 是
是![]() 中点,现将
中点,现将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置.
的位置.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(Ⅰ)见证明;(Ⅱ)![]()
【解析】
第(Ⅰ)问先证![]() 平面
平面![]() ,由线面垂直证明面面垂直;
,由线面垂直证明面面垂直;
第(Ⅱ)问先找垂直关系后建立空间直角坐标系,利用向量法求出两面的法向量,进而求所成二面角的余弦值.
解:(Ⅰ)证明:∵![]() ,
,![]() ,点
,点![]() 是
是![]() 中点,
中点,
∴![]() ,
,![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(Ⅱ)由(Ⅰ)知![]() 平面
平面![]() ,
,
∴![]() 即为
即为![]() 与平面
与平面![]() 所成的角,
所成的角,
∴![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() 为等腰直角三角形,∴
为等腰直角三角形,∴![]() ,
,
故![]() 为等边三角形,
为等边三角形,
取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]() ,
,
∵![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
以![]() 为坐标原点,过点
为坐标原点,过点![]() 与
与![]() 平行的直线为
平行的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴建立空间直角坐标系如图,
轴建立空间直角坐标系如图,
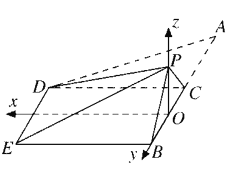
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
从而![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则由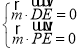 得
得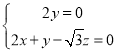 ,令
,令![]() 得
得![]() ,
,
又平面![]() 的一个法向量
的一个法向量![]() ,
,
则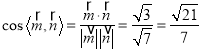 ,
,
所以,平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)若![]() ,求直线
,求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 有两个不同的交点,求
有两个不同的交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点,点M为BB1的中点.
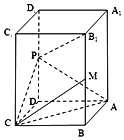
(1)求证:PB1⊥平面PAC;
(2)求直线CM与平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动队从![]() 四位运动员中选拔一人参加某项赛事,在选拔结果公布前,甲、乙、丙、丁四位教练对这四位运动员预测如下:甲说:“是
四位运动员中选拔一人参加某项赛事,在选拔结果公布前,甲、乙、丙、丁四位教练对这四位运动员预测如下:甲说:“是![]() 或
或![]() 被选中”; 乙说:“是
被选中”; 乙说:“是![]() 被选中”;丙说:“
被选中”;丙说:“![]() ,
,![]() 均未被选中”; 丁说:“是
均未被选中”; 丁说:“是![]() 被选中”.若这四位教练中只有两位说的话是对的,则获得参赛资格的运动员是____.
被选中”.若这四位教练中只有两位说的话是对的,则获得参赛资格的运动员是____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果底面是菱形的直棱柱(侧棱与底面垂直的棱柱)![]() 的所有棱长都相等,
的所有棱长都相等,![]() ,E,M,N分别为
,E,M,N分别为![]()
![]()
![]() 的中点,现有下列四个结论:①
的中点,现有下列四个结论:①![]() 平面
平面![]() ②
②![]() ③
③![]() 平面
平面![]() ④异面真线
④异面真线![]() 与MN所成的角的余弦值为
与MN所成的角的余弦值为![]() ,其中正确结论的个数为( )
,其中正确结论的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在常数![]() ,使得对定义域
,使得对定义域![]() 内的任意
内的任意![]() ,都有
,都有![]() 成立,则称函数
成立,则称函数![]() 在其定义域
在其定义域 ![]() 上是“
上是“![]() 利普希兹条件函数”.
利普希兹条件函数”.
(1)若函数![]() 是“
是“![]() 利普希兹条件函数”,求常数
利普希兹条件函数”,求常数![]() 的最小值;
的最小值;
(2)判断函数![]() 是否是“
是否是“![]() 利普希兹条件函数”,若是,请证明,若不是,请说明理由;
利普希兹条件函数”,若是,请证明,若不是,请说明理由;
(3)若![]() 是周期为2的“
是周期为2的“![]() 利普希兹条件函数”,证明:对任意的实数
利普希兹条件函数”,证明:对任意的实数![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了50人,他们年龄大点频率分布及支持“生育二胎”人数如下表:
年龄 |
|
|
|
|
|
|
频率 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
(1)由以上统计数据填下面2乘2列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异:

(2)若对年龄在![]() 的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的飞速发展,人民生活水平得到很大提高,汽车已经进入千千万万的家庭.大部分的车主在购买汽车时,会在轿车或者![]() 中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
购买了轿车(辆) | 购买了 | |
|
|
|
|
|
|
(1)根据表,是否有![]() 的把握认为年龄与购买的汽车车型有关?
的把握认为年龄与购买的汽车车型有关?
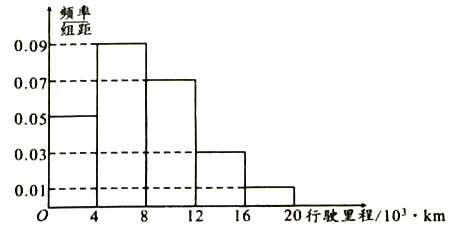
(2)图给出的是![]() 名车主上一年汽车的行驶里程,求这
名车主上一年汽车的行驶里程,求这![]() 名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
(3)用分层抽样的方法从![]() 岁以上车主中抽取
岁以上车主中抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人赠送免费保养券,求这
人赠送免费保养券,求这![]() 人中至少有
人中至少有![]() 辆轿车的概率。
辆轿车的概率。
附:![]() ,
,![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 汉字听写大会
汉字听写大会![]() 不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试
不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试![]() 现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组
现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,
,![]() ,第6组
,第6组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

![]() 若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
![]() 试估计该市市民正确书写汉字的个数的平均数与中位数;
试估计该市市民正确书写汉字的个数的平均数与中位数;
![]() 已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com