
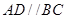 ,
,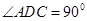 ,平面
,平面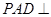 底面
底面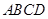 ,
,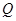 为
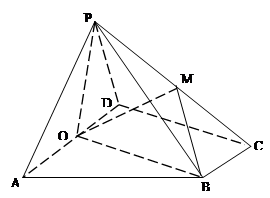
为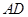 中点,M是棱PC上的点,
中点,M是棱PC上的点,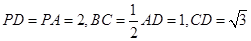 .
.
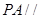 平面
平面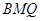 ;
;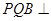 底面
底面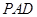 ;
;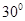 ,设PM=tMC,试确定t的值.
,设PM=tMC,试确定t的值.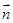 ,并设
,并设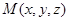 ,利用关系PM=tMC,用坐标表示出来,列方程解出
,利用关系PM=tMC,用坐标表示出来,列方程解出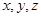 ,并得
,并得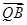 ,
, ,从而易得平面MBQ法向量为
,从而易得平面MBQ法向量为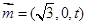 ,再由数量积运算得
,再由数量积运算得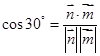 ,可得t值.
,可得t值.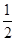 AD,即BC
AD,即BC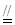 AQ.∴四边形BCQA为平行四边形,且N为AC中点,
AQ.∴四边形BCQA为平行四边形,且N为AC中点,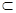 平面MQB,PA
平面MQB,PA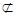 平面MQB, 3分
平面MQB, 3分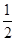 AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD // BQ . 6分
AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD // BQ . 6分 平面PQB,∴平面PQB⊥平面PAD. 9分
平面PQB,∴平面PQB⊥平面PAD. 9分 AD,Q为AD的中点∴ BC // DQ 且BC= DQ,
AD,Q为AD的中点∴ BC // DQ 且BC= DQ,  平面PAD,∴平面PQB⊥平面PAD. 9分
平面PAD,∴平面PQB⊥平面PAD. 9分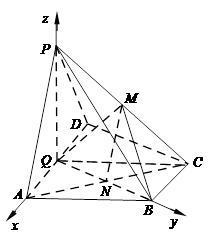
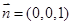 ;
;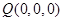 ,
,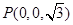 ,
,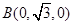 ,
,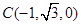 . 11分
. 11分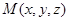 ,
,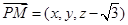 ,
,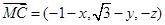 ,∵
,∵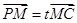 ,
,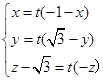 , ∴
, ∴ 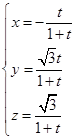 , 12分
, 12分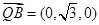 ,
,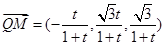 ,
,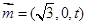 . 13分
. 13分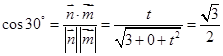 ,∴
,∴ 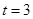 . 14分
. 14分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
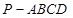 的底面是正方形,
的底面是正方形,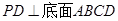 ,点
,点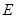 在棱
在棱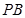 上.
上.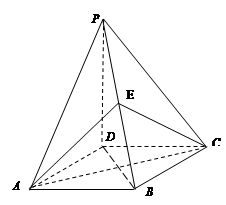
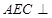 平面
平面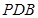 ;
;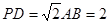 ,且
,且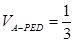 时,确定点
时,确定点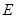 的位置,即求出
的位置,即求出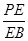 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
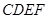 中,
中,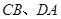 是梯形的高,
是梯形的高,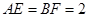 ,
,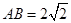 ,现将梯形沿
,现将梯形沿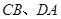 折起,使
折起,使 ,且
,且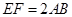 ,得一简单组合体
,得一简单组合体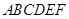 如图所示,已知
如图所示,已知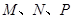 分别为
分别为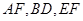 的中点.
的中点.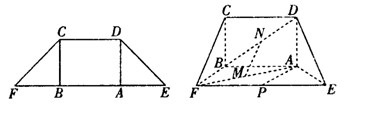
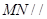 平面
平面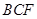 ;
; 平面
平面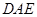 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
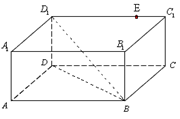
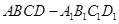 中,底面
中,底面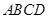 为正方形,
为正方形,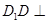 面
面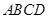 ,
,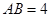 ,
,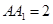 ,点
,点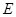 在棱
在棱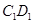 上,且
上,且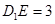 .
.
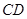 上确定一点
上确定一点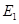 ,使得直线
,使得直线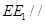 平面
平面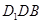 ,并证明;
,并证明;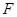 在底面
在底面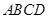 内,且
内,且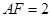 ,请说明点
,请说明点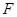 的轨迹,并探求
的轨迹,并探求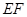 长度的最小值.
长度的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
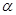 、
、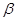 和直线
和直线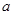 、
、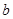 ,若
,若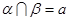 ,
,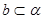 且
且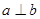 ,则
,则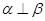 .
.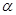 、
、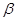 和两异面直线
和两异面直线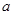 、
、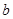 ,若
,若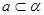 ,
,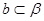 且
且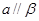 ,
,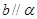 ,则
,则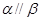 .
.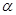 、
、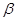 、
、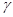 和直线
和直线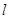 ,若
,若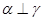 ,
,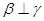 且
且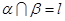 ,则
,则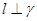 .
.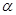 、
、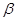 和直线
和直线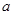 ,若
,若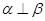 且
且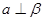 ,则
,则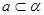 或
或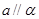 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com