
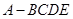 中,底面
中,底面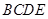 为矩形,侧面
为矩形,侧面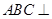 底面
底面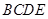 ,
,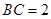 ,
,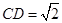 ,
,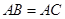 .
.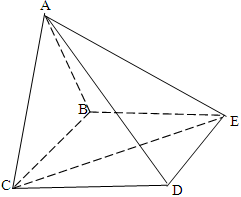
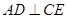 ;
; 与平面
与平面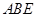 所成的角为
所成的角为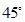 ,
, 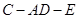 的余弦值.
的余弦值.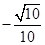 。
。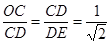 知,Rt△OCD∽Rt△CDE,
知,Rt△OCD∽Rt△CDE,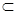 侧面ABE,所以侧面ABE⊥侧
侧面ABE,所以侧面ABE⊥侧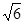 ,得CF=
,得CF=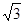
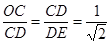 知,Rt△OCD∽Rt△CDE,从而∠ODC=∠CED,于是CE⊥OD,
知,Rt△OCD∽Rt△CDE,从而∠ODC=∠CED,于是CE⊥OD,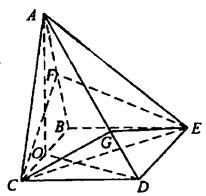
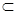 侧面ABE,所以侧面ABE⊥侧
侧面ABE,所以侧面ABE⊥侧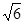 ,得CF=
,得CF=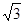
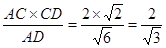
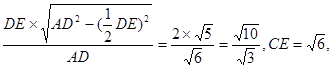
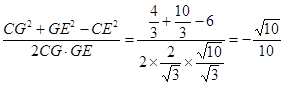
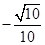 ---------------------12分
---------------------12分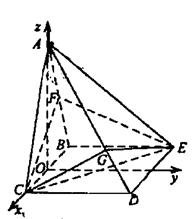
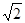 ,0), E(-1,
,0), E(-1, 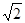 ,0),
,0),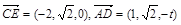 ,
,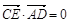 ,得AD⊥CE------------------4分
,得AD⊥CE------------------4分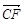 =(x-1,0,z),
=(x-1,0,z),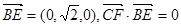 故CF⊥BE,又AB∩BE=B,所以CF⊥平面ABE,∠CEF是CE与平面ABE所成的角,∠CEF=45°
故CF⊥BE,又AB∩BE=B,所以CF⊥平面ABE,∠CEF是CE与平面ABE所成的角,∠CEF=45°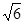 ,得CF=
,得CF=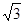 ,又CB=2,所以∠FBC=60°,△ABC为等边三角形,
,又CB=2,所以∠FBC=60°,△ABC为等边三角形,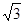 )作CG⊥AD,垂足为G,连接GE,在Rt△ACD中,求得|AG|=
)作CG⊥AD,垂足为G,连接GE,在Rt△ACD中,求得|AG|=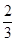 |AD|
|AD| )
)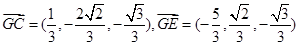
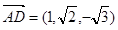 ,
,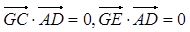
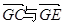 的夹角等于二面角C-AD-E的平面角。
的夹角等于二面角C-AD-E的平面角。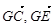 )=
)=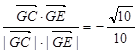
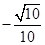 ---------12分
---------12分

科目:高中数学 来源:不详 题型:解答题
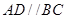 ,
,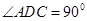 ,平面
,平面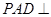 底面
底面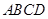 ,
,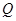 为
为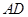 中点,M是棱PC上的点,
中点,M是棱PC上的点,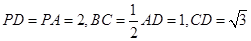 .
.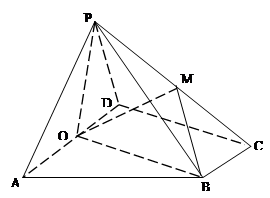
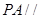 平面
平面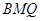 ;
;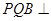 底面
底面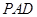 ;
;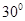 ,设PM=tMC,试确定t的值.
,设PM=tMC,试确定t的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
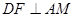 ,垂足为E,若将
,垂足为E,若将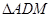 沿AM折起,使点D位于
沿AM折起,使点D位于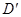 位置,连接
位置,连接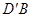 ,
,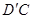 得四棱锥
得四棱锥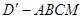 .
.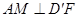 ;(2)若
;(2)若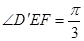 ,直线
,直线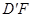 与平面ABCM所成角的大小为
与平面ABCM所成角的大小为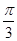 ,求直线
,求直线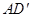 与平面ABCM所成角的正弦值.
与平面ABCM所成角的正弦值.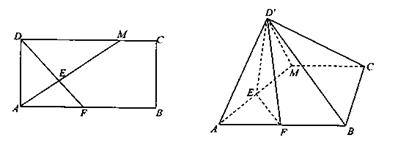
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
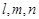 表示不同的直线,
表示不同的直线,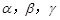 表示不同的平面,给出下列四个命题:
表示不同的平面,给出下列四个命题: 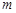 ∥
∥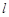 ,且
,且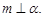 则
则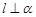 ;
; 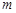 ∥
∥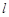 ,且
,且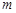 ∥
∥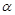 .则
.则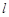 ∥
∥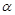 ;
;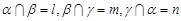 ,则
,则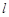 ∥m∥n;
∥m∥n; 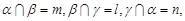 且n∥
且n∥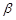 ,则
,则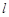 ∥m.
∥m.| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com