
���� ��1�����оٷ���ô�6�������������3�������л����¼�����10������������3����Ϊ����Ļ����¼�ֻ��1�����ɴ����������3����Ϊ����ĸ��ʣ�
��2���ɣ�1���ɵã�����ͬһ��ɫ��3����Ļ����¼���2�������÷�ͬһ��ɫ��3����Ļ����¼���18�������һ����̯����Ǯ100��$\frac{18}{20}$-100��$\frac{2}{20}$��5�����㼴�ɣ�
��� �⣺��3ֻ��ɫƹ������ΪA��B��C��3ֻ��ɫ��ƹ������Ϊ1��2��3����6�������������3���Ļ����¼�Ϊ��ABC��AB1��AB2��AB3��AC1��AC2��AC3��A12��A13��A23��BC1��BC2��BC3��B12��B13��B23��C12��C13��C23��123����20��
��1���¼�E={������3����Ϊ����}���¼�E�����Ļ����¼���1����������123��
P��E��=$\frac{1}{20}$=0.05
��2���ɣ�1���ɵã�����ͬһ��ɫ��3����Ļ����¼���2�������÷�ͬһ��ɫ��3����Ļ����¼���18����
�ٶ�һ������100�˴�������̯��Ǯ100��$\frac{18}{20}$-100��$\frac{2}{20}$��5=90-50=40 Ԫ��
���� ���⿼��Ҫ��ŵ�������⣬�����оٳ����鷢���������¼��������������¼����оٷ����ǽ���ŵ���������һ����Ҫ�Ľ��ⷽ���������е���


 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
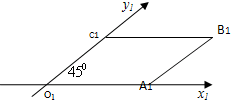 ��ͼ��һ��������OABC��б���⻭���µ�ֱ��ͼ�Ǹ�һ���߳�Ϊ1��ƽ���ı��Σ���������OABC�����Ϊ��������
��ͼ��һ��������OABC��б���⻭���µ�ֱ��ͼ�Ǹ�һ���߳�Ϊ1��ƽ���ı��Σ���������OABC�����Ϊ��������| A�� | 1 | B�� | 4 | C�� | 1��4 | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{119}{169}$ | B�� | -$\frac{1}{3}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{119}{169}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 15 | B�� | 10 | C�� | 7.5 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3�� | B�� | 6�� | C�� | 12�� | D�� | 24�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 6$\sqrt{2}$ | C�� | 8 | D�� | 8$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com