练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知△ABC的周长为4（
    		2
    +1），且sinB+sinC=
    		2
    sinA．
    （1）求边长a的值；
    （2）若S△ABC=3sinA，求角A的大小（结果用反三角函数值表示）．
    考点：正弦定理,反三角函数的运用
    专题：解三角形
    分析：（1）利用正弦定理，将角转化为边之间的关系，利用周长即可求出a的值．
    （2）利用三角形的面积公式，求出b，c的关系，利用余弦定理即可求出A的大小．
    解答： 解：（1）∵sinB+sinC=
    		2
    sinA，
    ∴由正弦定理得，b+c=
    		2
    a，（*）
    ∵a+b+c=4（
    		2
    +1），
    ∴解得a=4；
    （2）由S△ABC=
    1
    2
    bcsinA=3sinA，得bc=6，
    两边平方（*）式，求得b2+c2=20，
    由余弦定理，cosA=
    b2+c2-a2
    2bc
    =
    20-16
    2×6
    =
    4
    12
    =
    1
    3
    ，
    故A=arccos
    1
    3
    ．
    点评：本题主要考查正弦定理和余弦定理的应用，要求熟练掌握正弦定理和余弦定理．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    甲、乙两机床加工同一种零件，抽检得到它们加工后的零件尺寸x（单位：cm）及个数，如下表：
    零件尺寸x 1.01 1.02 1.03 1.04 1.05
    零件个数y 甲 3 7 8 9 3
    乙 7 4 4 4 a
    由表中数据得y关于x的线性回归方程为y=-91+l00x（1.01≤x≤1.05），其中合格零件尺寸为1.03±0.0l（cm）．
    （Ⅰ）完成下面列联表，并判断是否有99%的把握认为加工零件的质量与甲、乙有关；
    合格零件数 不合格零件数 合计
    甲
    乙
    合计
    （Ⅱ）从甲、乙加工后尺寸大于1.03cm的零件中各取1个，求恰好取到2个都是不合格零件的概率．附：参考公式及临界值表．
    K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ，其中n=a+b+c+d．
    P（K2≥k） 0.15 0.10 0.05 0.025 0.010 0.005 0.001
    k 2.072 2.706 3.841 5.024 6.635 7.879 10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系xoy中，已知四点A（
    		2
    ，
    		3
    ），B（-2，0），C（
    		6
    ，1），D（-
    		2
    ，-
    		3
    ）中有且只有三点在椭圆E： 
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）上．
    （1）求椭圆E的方程；
    （2）若P是圆x2+y2=12上的一个动点，过动点P作直线l1、l2，使得l1、l2与椭圆E都相切，求证：l1⊥l2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    		x-2
    的定义域为A，函数g（x）=
    2
    x
    （1≤x≤2）的值域为B．
    （Ⅰ）求A∩B；
    （Ⅱ）若C={y|a＜y＜2a-1}，且C⊆B，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知抛物线的方程为y=ax2-1，直线l的方程为y=
    x
    2
    ，点A（3，-1）关于直线l的对称点在抛物线上．
    （1）求抛物线的方程；
    （2）已知P（
    1
    2
    ，1），点F（0，-
    15
    16
    ）是抛物线的焦点，M是抛物线上的动点，求|MP|+|MF|的最小值及此时点M的坐标；
    （3）设点B、C是抛物线上的动点，点D是抛物线与x轴正半轴交点，△BCD是以D为直角顶点的直角三角形．试探究直线BC是否经过定点？若经过，求出定点的坐标；若不经过，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

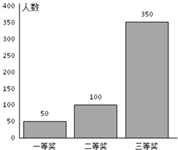    某超市进行促销活动，规定消费者消费每满100元可抽奖一次．抽奖规则：从装有三种只有颜色不同的球的袋中随机摸出一球，记下颜色后放回，依颜色分为一、二、三等奖，一等奖奖金15元，二等奖奖金10元，三等奖奖金5元．活动以来，中奖结果统计如图所示．消费者甲购买了238元的商品，准备参加抽奖．以频率作为概率，解答下列各题．
    （Ⅰ）求甲恰有一次获得一等奖的概率；
    （Ⅱ）求甲获得20元奖金的概率；
    （Ⅲ）记甲获得奖金金额为X，求X的分布列及期望EX．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    椭圆C：
    x2
    a2
    +
    y2
    b2
    =1过点A（1，
    3
    2
    ），离心率为
    1
    2
    ，左右焦点分别为F1、F2．过点F1的直线l交椭圆于A、B两点．
    （1）求椭圆C的方程．
    （2）当△F2AB的面积为
    12
    		2
    7
    时，求l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    点M是边长为2
    		2
    的正方形ABCD内或边界上一动点，N是边BC的中点，则
    AN
    •
    AM
    的最大值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    过点（0，1）作直线，使它与抛物线y2=4x仅有一个公共点，这样的直线有
     
    条．

    查看答案和解析>>

    同步练习册答案