
分析 (1)求出函数的导数,由导数大于0,可得增区间;导数小于0,可得减区间;
(2)求出函数的导数,设出切点,由切线的方程可得切线的斜率,和切点,解方程即可得到a的值;
(3)由g(x)=xlnx-a(x-1),知g'(x)=lnx+1-a,当0<a≤1时,g'(x)≥0,g(x)是增函数,最大值是g(e)=e-a(e-1);当a≥2时,g'(x)≤0,g(x)是减函数,最大值是g(1)=0;当1<a<2时,g(x)先减后增,最大值是g(1)或g(e).由此能求出g(x)在区间[1,e]上的最大值.
解答 解:(1)∵函数f(x)=$\frac{a(x-1)}{{x}^{2}}$,
∴f′(x)=$\frac{a{x}^{2}-2ax(x-1)}{{x}^{4}}$=$\frac{2a-ax}{{x}^{3}}$,
∵a>0,
∴由f′(x)=$\frac{2a-ax}{{x}^{3}}$>0,
得$\left\{\begin{array}{l}{2a-ax>0}\\{{x}^{3}>0}\end{array}\right.$,或$\left\{\begin{array}{l}{2a-ax<0}\\{{x}^{3}<0}\end{array}\right.$,
∴0<x<2,或无解,
∴函数f(x)的单调增区间为(0,2).
由f′(x)=$\frac{2a-ax}{{x}^{3}}$<0,
得$\left\{\begin{array}{l}{2a-ax<0}\\{{x}^{3}>0}\end{array}\right.$,或$\left\{\begin{array}{l}{2a-ax>0}\\{{x}^{3}<0}\end{array}\right.$,
∴x>2或x<0.
∴函数f(x)的单调减区间为(-∞,0)和(2,+∞).
(2)f(x)=$\frac{a(x-1)}{{x}^{2}}$的导数为f′(x)=$\frac{a{x}^{2}-2ax(x-1)}{{x}^{4}}$=$\frac{2a-ax}{{x}^{3}}$,
设切点为(m,n),可得切线的斜率为$\frac{2a-am}{{m}^{3}}$=1,
且n=m-1=$\frac{a(m-1)}{{m}^{2}}$,
解得m=1,n=0,a=1.
则a的值为1;
(3)∵f(x)=$\frac{a(x-1)}{{x}^{2}}$,g(x)=xlnx-x2f(x),
∴g(x)=xlnx-a(x-1),
∴g'(x)=lnx+1-a,
当0<a≤1时,g'(x)≥0,g(x)是增函数,最大值是g(e)=e-a(e-1);
当a≥2时,g'(x)≤0,g(x)是减函数,最大值是g(1)=0;
当1<a<2时,g(x)先减后增,最大值是g(1)或g(e).
设g(1)>g(e),即 e-a(e-1)<0,即 a>$\frac{e}{e-1}$,
所以若$\frac{e}{e-1}$<a<2 时,最大值是g(1),
若1<a<$\frac{e}{e-1}$,最大值是g(e).
综上,0<a<$\frac{e}{e-1}$时,最大值是g(e)=e-a(e-1);
$\frac{e}{e-1}$<a<2 时,最大值是g(1)=0.
点评 本题考查导数的运用:函数的单调区间和切线的求法和函数在闭区间上的最大值.综合性强,是高考的重点.解题时要认真解答,注意导数性质的灵活运用.易错点是分类不清,导致出错.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
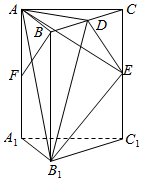 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=1,AC=$\sqrt{3}$,AA1=4,点D、E、F分别是棱BC、CC1、AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=1,AC=$\sqrt{3}$,AA1=4,点D、E、F分别是棱BC、CC1、AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com