
分析 (1)利用向量平行,求得tanx=-$\frac{3}{4}$,二倍角公式cos2x=cos2x-sin2x═$\frac{1-2tanx}{ta{n}^{2}x+1}$,可求得,
(2)将f(x)化简得f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+$\frac{3}{2}$,根据正弦函数的性质,求得f(x)的最大值及x的取值.
解答 解:(1)当$\overrightarrow{a}$∥$\overrightarrow{b}$时,-sinx=$\frac{3}{4}cosx$,
tanx=-$\frac{3}{4}$,
cos2x=cos2x-sin2x=$\frac{co{s}^{2}x-si{n}^{2}x}{si{n}^{2}x+co{s}^{2}x}$=$\frac{co{s}^{2}x-2sinxcosx}{si{n}^{2}x+co{s}^{2}x}$,
=$\frac{1-2tanx}{ta{n}^{2}x+1}$,
=$\frac{8}{5}$,
(2)设函数f(x)=2($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{b}$=2sinxcosx+2cos2+$\frac{1}{2}$,
=sin2x+cos2x+$\frac{3}{2}$,
=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+$\frac{3}{2}$,
0≤x≤$\frac{π}{2}$时,$\frac{π}{4}$≤2x+$\frac{π}{4}$≤$\frac{5π}{4}$,
当x=$\frac{π}{8}$时,f(x)的最大值为$\sqrt{2}+\frac{3}{2}$.
点评 本题考查向量数量积的坐标表示和三角函数的性质,属于中档题.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
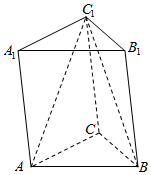 如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥C1-ABC的体积为$\frac{\sqrt{3}}{12}$.
如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥C1-ABC的体积为$\frac{\sqrt{3}}{12}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
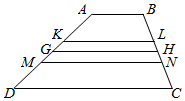 如图,四边形ABCD为梯形,其中AB=a,CD=b,若GH表示平行于两底且与它们等距离的线段(即梯形的中位线),KL表示平行于两底且使梯形ABLK与梯形KLCD相似的线段,MN表示平行于两底且将梯形ABCD分为面积相等的两个梯形的线段.
如图,四边形ABCD为梯形,其中AB=a,CD=b,若GH表示平行于两底且与它们等距离的线段(即梯形的中位线),KL表示平行于两底且使梯形ABLK与梯形KLCD相似的线段,MN表示平行于两底且将梯形ABCD分为面积相等的两个梯形的线段.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
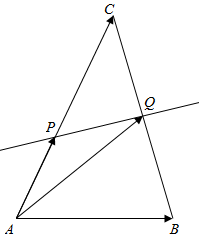 如图,已知△ABC的边BC的垂直平分线交AC于点P,交BC于点Q,若|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=5,则($\overrightarrow{AP}$+$\overrightarrow{AQ}$)•($\overrightarrow{AB}$-$\overrightarrow{AC}$)的值为-16.
如图,已知△ABC的边BC的垂直平分线交AC于点P,交BC于点Q,若|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=5,则($\overrightarrow{AP}$+$\overrightarrow{AQ}$)•($\overrightarrow{AB}$-$\overrightarrow{AC}$)的值为-16.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | ($\frac{35}{6}$,+∞) | C. | (-∞,0] | D. | (-∞,$\frac{3}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com