
在平面直角坐标系中,若 ,且
,且 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)已知定点 ,若斜率为
,若斜率为 的直线
的直线 过点
过点 并与轨迹
并与轨迹 交于不同的两点
交于不同的两点 ,且对于轨迹
,且对于轨迹 上任意一点
上任意一点 ,都存在
,都存在 ,使得
,使得 成立,试求出满足条件的实数
成立,试求出满足条件的实数 的值.
的值.
(1)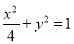 ;(2)
;(2)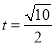 .
.
【解析】
试题分析:(1)设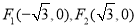 ,则
,则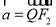 ,
,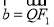 ,由
,由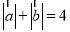 可得
可得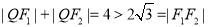 ,结合椭圆的定义可知,动点
,结合椭圆的定义可知,动点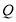 的轨迹是以
的轨迹是以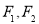 为焦点,4为长轴长的椭圆,从而可以确定椭圆标准方程中的参数
为焦点,4为长轴长的椭圆,从而可以确定椭圆标准方程中的参数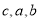 的取值,进而写出椭圆的方程即可;(2)设
的取值,进而写出椭圆的方程即可;(2)设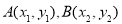 ,直线
,直线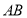 :
: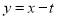 ,联立直线
,联立直线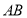 的方程与(1)中椭圆的方程,消去
的方程与(1)中椭圆的方程,消去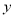 得到
得到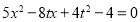 ,进而根据
,进而根据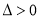 得
得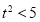 ,且
,且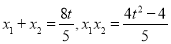 ,再计算出
,再计算出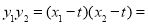
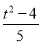 ,然后由
,然后由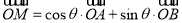 确定
确定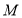 的横纵坐标,根据点
的横纵坐标,根据点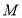 在轨迹
在轨迹 上,将点
上,将点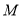 的坐标代入轨迹
的坐标代入轨迹 的方程并由
的方程并由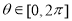 的任意性,得到
的任意性,得到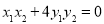 即
即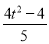
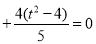 ,从中求解,并结合
,从中求解,并结合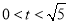 即可得到满足要求的
即可得到满足要求的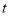 的值.
的值.
试题解析:(1)设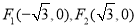 ,则
,则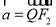 ,
,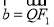
由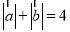 可得
可得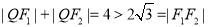
∴动点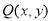 到两个定点
到两个定点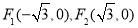 的距离的和为4
的距离的和为4
∴轨迹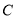 是以
是以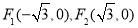 为焦点的椭圆,且长轴长为
为焦点的椭圆,且长轴长为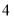
设该椭圆的方程为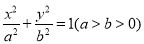
则有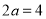 且
且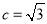 ,所以
,所以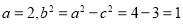
所以轨迹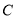 的方程为
的方程为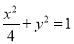
(2)设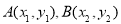 ,直线
,直线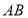 的方程为
的方程为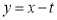 ,代入
,代入
消去 得
得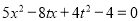
由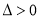 得
得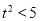 ,且
,且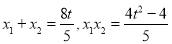
∴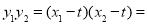
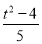
设点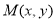 ,由
,由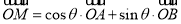 可得
可得
∵点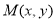 在
在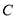 上
上
∴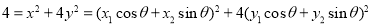
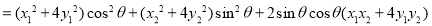
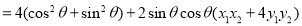
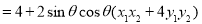
∴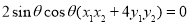
又因为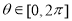 的任意性,∴
的任意性,∴
∴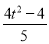
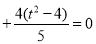 ,又
,又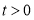 ,得
,得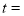
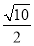
代入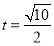 检验,满足条件,故
检验,满足条件,故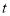 的值是
的值是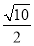 .
.
考点:1.动点的轨迹问题;2.椭圆的定义及其标准方程;3.直线与圆锥曲线的综合问题.


科目:高中数学 来源:2015届四川省成都市高三九月月考文科数学试卷(解析版) 题型:选择题
“ ”是“
”是“ ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届四川成都树德中学高二3月月考理科数学试卷(解析版) 题型:填空题
椭圆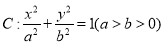 的左,右焦点分别为
的左,右焦点分别为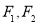 ,焦距为
,焦距为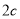 ,若直线
,若直线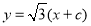 与椭圆
与椭圆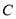 的一个交点
的一个交点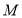 满足
满足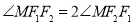 ,则该椭圆的离心率为 .
,则该椭圆的离心率为 .
查看答案和解析>>
科目:高中数学 来源:2015届四川成都树德中学高二3月月考文科数学试卷(解析版) 题型:解答题
已知命题 :方程
:方程 有两个不相等的负实根,命题
有两个不相等的负实根,命题 :
:
 恒成立;若
恒成立;若 或
或 为真,
为真, 且
且 为假,求实数
为假,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届四川成都树德中学高二3月月考文科数学试卷(解析版) 题型:选择题
已知椭圆 和双曲线
和双曲线 有相同的焦点
有相同的焦点 ,点
,点 为椭圆和双曲线的一个交点,则
为椭圆和双曲线的一个交点,则 的值为( )
的值为( )
A.16 B.25 C.9 D.不为定值
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次任意抽取3道题,独立作答,然后由乙回答剩余3题,每人答对其中的2题就停止答题,即闯关成功。已知6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是 .
.
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com