
| 3 |
| 2 |
| 13 |
| 3 |
A、f(1)<f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|
| 13 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
| 3 |
| 2 |
| 5 |
| 3 |
| 3 |
| 2 |
| 5 |
| 3 |
| 13 |
| 3 |
| 3 |
| 2 |


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
| A、p∧q |
| B、(¬p)∨(¬q) |
| C、(¬p)∧q |
| D、p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、直角三角形绕其一边旋转形成圆锥 |
| B、等边三角形绕其一边旋转形成圆锥 |
| C、平面截圆锥所得的图形是圆 |
| D、过圆锥顶点的截面图形是等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、①② | B、②③ | C、①③ | D、①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:
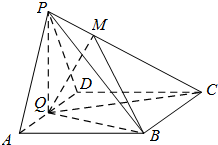 如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,平面PAD⊥平面ABCD,PA=PD=AD=2,Q为AD的中点,M是棱PC上一点,且PM=
如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,平面PAD⊥平面ABCD,PA=PD=AD=2,Q为AD的中点,M是棱PC上一点,且PM=| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
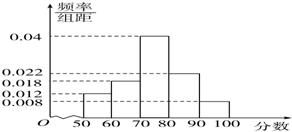 某市的教育研究机构对全市高三学生进行综合素质测试,随机抽取了部分学生的成绩,得到如图所示的成绩频率分布直方图.
某市的教育研究机构对全市高三学生进行综合素质测试,随机抽取了部分学生的成绩,得到如图所示的成绩频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:
1+2sin(π-α)sin(
| ||
cos2(
|
| ||
| (4cos212°-2)sin12° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com