
| A. | (-∞,2] | B. | $[-\frac{5}{2},+∞)$ | C. | $(-∞,-\frac{5}{2})∪(2,+∞)$ | D. | $(-∞,-\frac{5}{2}]∪[2,+∞)$ |
分析 命题p真:函数f(x)=lnx+$\frac{1}{2}{x^2}$-ax的导数f′(x)=$\frac{1}{x}+x-a$≥0在(0,+∞)上恒成立,∴a≤($\frac{1}{x}+x$)min;
命题q真:对?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),等价于f(x)min≥g(x)min,于是问题转化为求函数f(x),g(x)的最小值问题.再根据p、q的真假,求出a即可.
解答 解:命题p真:函数f(x)=lnx+$\frac{1}{2}{x^2}$-ax的导数f′(x)=$\frac{1}{x}+x-a$≥0在(0,+∞)上恒成立,
∴a≤($\frac{1}{x}+x$)min,⇒a≤2;
命题q真:当x∈[1,2]时,函数f(x)=x2+$\frac{2}{x}$=x2+$\frac{1}{x}+\frac{1}{x}$≥3$\root{3}{{x}^{2}•\frac{1}{x}•\frac{1}{x}}=3$,所以f(x)min=3;
g(x)=($\frac{1}{2}$)x-a在[-1,1]上单调递减,所以g(x)min=g(1),
对?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),
等价于f(x)min≥g(x)min,即3≥$\frac{1}{2}-a$,解得a≥-$\frac{5}{2}$
若命题p∨q为真命题,命题p∧q为假命题⇒p、q为一真一假,
当p真,q假时,解得a<-$\frac{5}{2}$,当p假,q真时,解得a>2.
综上:实数a的取值范围是:a<-$\frac{5}{2}$或a>2.
故选:C.
点评 本题考查了利用导数研究函数的单调性,及函数恒成立,转化思想是关键,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
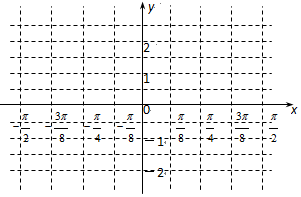 已知函数$f(x)=2cosxsin({x+\frac{π}{3}})-\sqrt{3}{sin^2}x+sinxcosx$.
已知函数$f(x)=2cosxsin({x+\frac{π}{3}})-\sqrt{3}{sin^2}x+sinxcosx$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,0) | B. | (-2,0) | C. | (0,2) | D. | (0,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com