
【题目】如图,已知圆![]() 经过椭圆
经过椭圆![]() 的左右焦点
的左右焦点![]() ,与椭圆
,与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
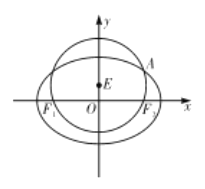
(1)求椭圆![]() 的方程;
的方程;
(2)设与直线![]() (
(![]() 为原点)平行的直线交椭圆
为原点)平行的直线交椭圆![]() 于
于![]() 两点,当
两点,当![]() 的面积取取最大值时,求直线
的面积取取最大值时,求直线![]() 的方程.
的方程.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由题意把焦点坐标代入圆的方程求出![]() ,再由条件得
,再由条件得![]() 为圆
为圆![]() 的直径,且
的直径,且![]() ,根据勾股定理求出
,根据勾股定理求出![]() ,根据椭圆的定义和
,根据椭圆的定义和![]() 依次求出
依次求出![]() 的值,代入椭圆方程即可;
的值,代入椭圆方程即可;
(2)由(1)求出![]() 的坐标,根据向量共线的条件求出直线
的坐标,根据向量共线的条件求出直线![]() 的斜率,设直线
的斜率,设直线![]() 的方程和
的方程和![]() 的坐标,联立直线方程和椭圆方程消去
的坐标,联立直线方程和椭圆方程消去![]() ,利用韦达定理和弦长公式求出
,利用韦达定理和弦长公式求出![]() ,由点到直线的距离公式求出点
,由点到直线的距离公式求出点![]() 到直线
到直线![]() 的距离,代入三角形的面积公式求出
的距离,代入三角形的面积公式求出![]() ,化简后求最值即可.
,化简后求最值即可.
试题解析:(1)∵![]() ,
, ![]() ,
, ![]() 三点共线,∴
三点共线,∴![]() 为圆
为圆![]() 的直径,且
的直径,且![]() ,
,
∴![]() .由
.由![]() ,得
,得![]() ,∴
,∴![]() ,∵
,∵![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
, ![]() .
.
∵![]() ,∴
,∴![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() . (2)由(1)知,点
. (2)由(1)知,点![]() 的坐标为
的坐标为![]() ,∴直线
,∴直线![]() 的斜率为
的斜率为![]() ,故设直线
,故设直线![]() 的方程为
的方程为![]() ,将
,将![]() 方程代入
方程代入![]() 消去
消去![]() 得:
得: ![]() , 设
, 设![]()
![]() ∴
∴![]() ,
, ![]() ,
, ![]() ,
,![]() ∴
∴![]() , 又:
, 又:
![]() =
=![]() ,∵点
,∵点![]() 到直线
到直线![]() 的距离
的距离![]() , ∴
, ∴![]()

![]()
![]() ,
,
当且仅当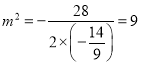 ,即
,即![]() 时等号成立,此时直线
时等号成立,此时直线![]() 的方程为
的方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】正方体![]() 的棱长为2,E,F,G分别为
的棱长为2,E,F,G分别为![]() ,
,![]() ,
,![]() 的中点,则( )
的中点,则( )
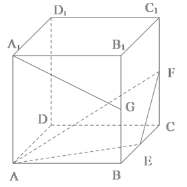
A.直线![]() 与直线
与直线![]() 垂直
垂直
B.直线![]() 与平面
与平面![]() 不平行
不平行
C.平面![]() 截正方体所得的截面面积为
截正方体所得的截面面积为![]()
D.点C与点G到平面![]() 的距离相等
的距离相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于曲线![]() ,给出下列三个结论:
,给出下列三个结论:
① 曲线![]() 关于原点对称,但不关于
关于原点对称,但不关于![]() 轴、
轴、![]() 轴对称;
轴对称;
② 曲线![]() 恰好经过4个整点(即横、纵坐标均为整数的点);
恰好经过4个整点(即横、纵坐标均为整数的点);
③ 曲线![]() 上任意一点到原点的距离都不大于
上任意一点到原点的距离都不大于![]() .
.
其中,正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中不正确的是( )
A.设![]() 为直线,
为直线,![]() 为平面,且
为平面,且![]() ;则“
;则“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
B.设随机变量![]() ,若
,若![]() ,则
,则![]()
C.若不等式![]() (
(![]() )恒成立,则
)恒成立,则![]() 的取值范围是
的取值范围是![]()
D.已知直线![]() 经过点
经过点![]() ,则
,则![]() 的取值范围是
的取值范围是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,得到甲、乙两位学生成绩的茎叶图.
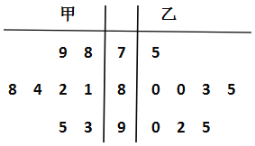
(1)现要从中选派一人参加数学竞赛,对预赛成绩的平均值和方差进行分析,你认为哪位学生的成绩更稳定?请说明理由;
(2)若将频率视为概率,求乙同学在一次数学竞赛中成绩高于84分的概率;
(3)求在甲同学的8次预赛成绩中,从不小于80分的成绩中随机抽取2个成绩,列出所有结果,并求抽出的2个成绩均大于85分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】雷达图(Radar Chart),又可称为戴布拉图、蜘蛛网图(Spider Chart),原先是财务分析报表的一种,现可用于对研究对象的多维分析.图为甲、乙两人在五个方面的评价值的雷达图,则下列说法不正确的是( )
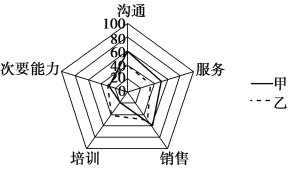
A.甲、乙两人在次要能力方面的表现基本相同
B.甲在沟通、服务、销售三个方面的表现优于乙
C.在培训与销售两个方面上,甲的综合表现优于乙
D.甲在这五个方面的综合表现优于乙
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年3月,国内新冠肺炎疫情得到有效控制,人们开始走出家门享受春光.某旅游景点为吸引游客,推出团体购票优惠方案如下表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
两个旅游团队计划游览该景点.若分别购票,则共需支付门票费1290元;若合并成个团队购票,则需支付门票费990元,那么这两个旅游团队的人数之差为( )
A.20B.30C.35D.40
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列![]() 和等比数列
和等比数列![]() 中,
中, ![]() ,
,![]() ,
,![]() 是
是![]() 前
前![]() 项和.
项和.
(1)若 ![]() ,求实数
,求实数![]() 的值;
的值;
(2)是否存在正整数![]() ,使得数列
,使得数列![]() 的所有项都在数列
的所有项都在数列![]() 中?若存在,求出所有的
中?若存在,求出所有的![]() ,若不存在,说明理由;
,若不存在,说明理由;
(3)是否存在正实数![]() ,使得数列
,使得数列![]() 中至少有三项在数列
中至少有三项在数列![]() 中,但
中,但![]() 中的项不都在数列
中的项不都在数列![]() 中?若存在,求出一个可能的
中?若存在,求出一个可能的![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com