
【题目】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,得到甲、乙两位学生成绩的茎叶图.
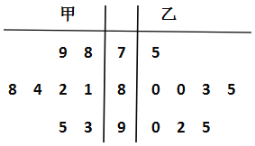
(1)现要从中选派一人参加数学竞赛,对预赛成绩的平均值和方差进行分析,你认为哪位学生的成绩更稳定?请说明理由;
(2)若将频率视为概率,求乙同学在一次数学竞赛中成绩高于84分的概率;
(3)求在甲同学的8次预赛成绩中,从不小于80分的成绩中随机抽取2个成绩,列出所有结果,并求抽出的2个成绩均大于85分的概率.
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为2,
的棱长为2,![]() 平面
平面![]() .平面
.平面![]() 截此正方体所得的截面有以下四个结论:
截此正方体所得的截面有以下四个结论:
①截面形状可能是正三角形②截面的形状可能是正方形
③截面形状可能是正五边形④截面面积最大值为![]()
则正确结论的编号是( )
A.①④B.①③C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2017年起,全国各省市陆续实施了新高考,许多省市采用了“![]() ”的选科模式,即:考生除必考的语数外三科外,再从物理化学生物历史地理政治六个学科中,任意选取三科参加高考,为了调查新高考中考生的选科情况,某地调查小组对某中学进行了一次调查,研究考生选择化学与选择物理是否有关.已知在调查数据中,选物理的考生与不选物理的考生人数相同,其中选物理且选化学的人数占选物理人数的
”的选科模式,即:考生除必考的语数外三科外,再从物理化学生物历史地理政治六个学科中,任意选取三科参加高考,为了调查新高考中考生的选科情况,某地调查小组对某中学进行了一次调查,研究考生选择化学与选择物理是否有关.已知在调查数据中,选物理的考生与不选物理的考生人数相同,其中选物理且选化学的人数占选物理人数的![]() ,在不选物理的考生中,选化学与不选化学的人数比为
,在不选物理的考生中,选化学与不选化学的人数比为![]() .
.
(1)若在此次调查中,选物理未选化学的考生有100人,将选物理且选化学的人数占选化学总人数的比作为概率,从该中学选化学的考生中随机抽取4人,记这4人中选物理且选择化学的考生人数为![]() ,求
,求![]() 的分布列(用排列数组合数表示即可)和数学期望.
的分布列(用排列数组合数表示即可)和数学期望.
(2)若研究得到在犯错误概率不超过0.01的前提下,认为选化学与选物理有关,则选物理且选化学的人数至少有多少?(单位:百人,精确到0.01)
附: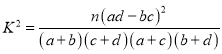 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆![]() 经过椭圆
经过椭圆![]() 的左右焦点
的左右焦点![]() ,与椭圆
,与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
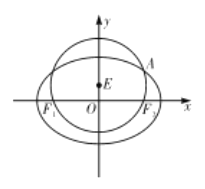
(1)求椭圆![]() 的方程;
的方程;
(2)设与直线![]() (
(![]() 为原点)平行的直线交椭圆
为原点)平行的直线交椭圆![]() 于
于![]() 两点,当
两点,当![]() 的面积取取最大值时,求直线
的面积取取最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(1+x)t﹣1的定义域为(﹣1,+∞),其中实数t满足t≠0且t≠1.直线l:y=g(x)是f(x)的图象在x=0处的切线.
(1)求l的方程:y=g(x);
(2)若f(x)≥g(x)恒成立,试确定t的取值范围;
(3)若a1,a2∈(0,1),求证: ![]() .注:当α为实数时,有求导公式(xα)′=αxα﹣1.
.注:当α为实数时,有求导公式(xα)′=αxα﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|2x+4|+|x-3|.
(1)解关于x的不等式f(x)<8;
(2)对于正实数a,b,函数g(x)=f(x)-3a-4b只有一个零点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,动直线
,动直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.![]() 为坐标原点,
为坐标原点,![]() 是
是![]() 中点.
中点.
(1)若![]() ,求
,求![]() 的面积;
的面积;
(2)若试探究是否存在常数![]() ,使得
,使得![]() 是定值?若存在,求
是定值?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com