
【题目】已知函数f(x)=(1+x)t﹣1的定义域为(﹣1,+∞),其中实数t满足t≠0且t≠1.直线l:y=g(x)是f(x)的图象在x=0处的切线.
(1)求l的方程:y=g(x);
(2)若f(x)≥g(x)恒成立,试确定t的取值范围;
(3)若a1,a2∈(0,1),求证: ![]() .注:当α为实数时,有求导公式(xα)′=αxα﹣1.
.注:当α为实数时,有求导公式(xα)′=αxα﹣1.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)根据函数的解析式求出导函数的解析式,求出切点坐标及切线的斜率(切点的导函数值),可得直线![]() 的方程;
的方程;
(2)构造函数![]() ,若
,若![]() 恒成立,即
恒成立,即![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上的最小值不小于0,分类讨论后可得满足条件的
上的最小值不小于0,分类讨论后可得满足条件的![]() 的取值范围;
的取值范围;
(3)分![]() 和
和![]() 两种情况证明结论,并构造函数
两种情况证明结论,并构造函数![]() ,先征得
,先征得![]() 是单调减函数,进而得到结论.
是单调减函数,进而得到结论.
(1)∵f(x)=(1+x)t﹣1
∴f'(x)=t(1+x)x﹣1,
∴f'(0)=t,
又f(0)=0,
∴l的方程为:y=tx;
(2)令h(x)=f(x)﹣g(x)=(1+x)t﹣tx﹣1,
h'(x)=t(1+x)t﹣1﹣t=t[(1+x)t﹣1﹣1]
当t<0时,(1+x)t﹣1﹣1单调递减,
当x=0时,h'(x)=0
当x∈(﹣1,0),h'(x)<0,h(x)单调递减;
当x∈(0,+∞),h'(x)>0,h(x)单调递增.
∴x=0是h(x)的唯一极小值点,
∴h(x)≥h(0)=0,f(x)≥g(x)恒成立;
当0<t<1时,(1+x)t﹣1﹣1单调递减,
当x=0时,h'(x)=0
当x∈(﹣1,0),h'(x)>0,h(x)单调递增;
当x∈(0,+∞),h'(x)<0,h(x)单调递减.
∴x=0是h(x)的唯一极大值点,
∴h(x)≤h(0)=0,不满足f(x)≥g(x)恒成立;
当t>1时,(1+x)t﹣1﹣1单调递增,
当x=0时,h'(x)=0
当x∈(﹣1,0),h'(x)<0,h(x)单调递减;
当x∈(0,+∞),h'(x)>0,h(x)单调递增.
∴x=0是h(x)的唯一极小值点,
∴h(x)≥h(0)=0,f(x)≥g(x)恒成立;
综上,t∈(﹣∞,0)∪(1,+∞);
证明:(3)当a1=a2,不等式显然成立;
当a1≠a2时,不妨设a1<a2
则![]()
![]()
令![]() ,x∈[a1,a2]
,x∈[a1,a2]
下证φ(x)是单调减函数:
∵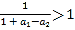
易知a1﹣a2∈(﹣1,0),1+a1﹣a2∈(0,1),![]()
由(2)知当t>1,(1+x)t>1+tx,x∈[a1,a2]
∴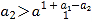
∴![]()
∴![]()
∴φ'(x)<0,
∴φ(x)在[a1,a2]上单调递减.
∴φ(a1)>φ(a2),
即![]()
∴![]() .
.
综上,![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】某企业现有A.B两套设备生产某种产品,现从A,B两套设备生产的大量产品中各抽取了100件产品作为样本,检测某一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.图1是从A设备抽取的样本频率分布直方图,表1是从B设备抽取的样本频数分布表.
内的产品视为合格品,否则为不合格品.图1是从A设备抽取的样本频率分布直方图,表1是从B设备抽取的样本频数分布表.
图1:A设备生产的样本频率分布直方图
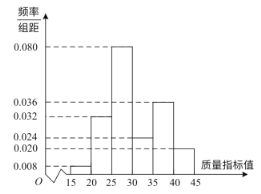
表1:B设备生产的样本频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 2 | 18 | 48 | 14 | 16 | 2 |
(1)请估计A.B设备生产的产品质量指标的平均值;
(2)企业将不合格品全部销毁后,并对合格品进行等级细分,质量指标值落在![]() 内的定为一等品,每件利润240元;质量指标值落在
内的定为一等品,每件利润240元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件利润180元;其它的合格品定为三等品,每件利润120元.根据图1、表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.企业由于投入资金的限制,需要根据A,B两套设备生产的同一种产品每件获得利润的期望值调整生产规模,请根据以上数据,从经济效益的角度考虑企业应该对哪一套设备加大生产规模?
内的定为二等品,每件利润180元;其它的合格品定为三等品,每件利润120元.根据图1、表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.企业由于投入资金的限制,需要根据A,B两套设备生产的同一种产品每件获得利润的期望值调整生产规模,请根据以上数据,从经济效益的角度考虑企业应该对哪一套设备加大生产规模?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于正整数![]() ,如果
,如果![]() 个整数
个整数![]() 满足
满足![]() ,
,
且![]() ,则称数组
,则称数组![]() 为
为![]() 的一个“正整数分拆”.记
的一个“正整数分拆”.记![]() 均为偶数的“正整数分拆”的个数为
均为偶数的“正整数分拆”的个数为![]() 均为奇数的“正整数分拆”的个数为
均为奇数的“正整数分拆”的个数为![]() .
.
(Ⅰ)写出整数4的所有“正整数分拆”;
(Ⅱ)对于给定的整数![]() ,设
,设![]() 是
是![]() 的一个“正整数分拆”,且
的一个“正整数分拆”,且![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)对所有的正整数![]() ,证明:
,证明:![]() ;并求出使得等号成立的
;并求出使得等号成立的![]() 的值.
的值.
(注:对于![]() 的两个“正整数分拆”
的两个“正整数分拆”![]() 与
与![]() ,当且仅当
,当且仅当![]() 且
且![]() 时,称这两个“正整数分拆”是相同的.)
时,称这两个“正整数分拆”是相同的.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解一个智力游戏是否与性别有关,从某地区抽取男女游戏玩家各200请客,其中游戏水平分为高级和非高级两种.
(1)根据题意完善下列![]() 列联表,并根据列联表判断是否有99%以上的把握认为智力游戏水平高低与性别有关?
列联表,并根据列联表判断是否有99%以上的把握认为智力游戏水平高低与性别有关?
性别 | 高级 | 非高级 | 合计 |
女 | 40 | ||
男 | 140 | ||
合计 |
(2)按照性别用分层抽样的方法从这些人中抽取10人,从这10人中抽取3人作为游戏参赛选手;
![]() 若甲入选了10人名单,求甲成为参赛选手的概率;
若甲入选了10人名单,求甲成为参赛选手的概率;
![]() 设抽取的3名选手中女生的人数为
设抽取的3名选手中女生的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附表: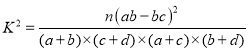 ,其中
,其中![]() .
.
| 0.010 | 0.05 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,得到甲、乙两位学生成绩的茎叶图.
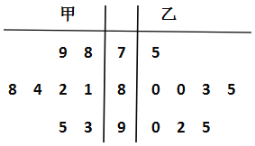
(1)现要从中选派一人参加数学竞赛,对预赛成绩的平均值和方差进行分析,你认为哪位学生的成绩更稳定?请说明理由;
(2)若将频率视为概率,求乙同学在一次数学竞赛中成绩高于84分的概率;
(3)求在甲同学的8次预赛成绩中,从不小于80分的成绩中随机抽取2个成绩,列出所有结果,并求抽出的2个成绩均大于85分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国际篮联篮球世界杯,将于2019年在的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传世界杯,某大学从全校学生中随机抽取了![]() 名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
会收看 | 不会收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根据上表说明,能否有![]() 的把握认为收看篮球世界杯赛事与性别有关?
的把握认为收看篮球世界杯赛事与性别有关?
(2)现从参与问卷调查且收看篮球世界杯赛事的学生中,采用按性别分层抽样的方法选取![]() 人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
(i)求男、女学生各选取多少人;
(ii)若从这![]() 人中随机选取
人中随机选取![]() 人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到
人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到![]() 名男生的概率.
名男生的概率.
附: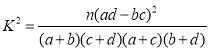 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国际篮联篮球世界杯将于2019年8月31日至9月15日在中国的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传国际篮联篮球世界杯,某大学从全校学生中随机抽取了120名学生,对是否会收看该国际篮联篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
会收看 | 不会收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根据上表说明,能否有99%的把握认为是否会收看该国际篮联篮球世界杯赛事与性别有关?
(2)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球3次均未命中的概率为
,且乙投球3次均未命中的概率为![]() .
.
(i)求乙投球的命中率![]() ;
;
(ii)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: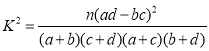 ,其中
,其中![]() ,
,
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高中生作文成绩与课外阅读量之间的关系,某研究机构随机抽取了100名高中生,根据问卷调查,得到以下数据:
作文成绩优秀 | 作文成绩一般 | 总计 | |
课外阅读量较大 | 35 | 20 | 55 |
课外阅读量一般 | 15 | 30 | 45 |
总计 | 50 | 50 | 100 |
(1)根据列联表,能否有99.5%的把握认为课外阅读量的大小与作文成绩优秀有关;
(2)若用分层抽样的方式从课外阅读量一般的高中生中选取了6名高中生,再从这6名高中生中随机选取2名进行面谈,求面谈的高中生中至少有1名作文成绩优秀的概率.
附: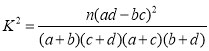 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com