
【题目】为了了解一个智力游戏是否与性别有关,从某地区抽取男女游戏玩家各200请客,其中游戏水平分为高级和非高级两种.
(1)根据题意完善下列![]() 列联表,并根据列联表判断是否有99%以上的把握认为智力游戏水平高低与性别有关?
列联表,并根据列联表判断是否有99%以上的把握认为智力游戏水平高低与性别有关?
性别 | 高级 | 非高级 | 合计 |
女 | 40 | ||
男 | 140 | ||
合计 |
(2)按照性别用分层抽样的方法从这些人中抽取10人,从这10人中抽取3人作为游戏参赛选手;
![]() 若甲入选了10人名单,求甲成为参赛选手的概率;
若甲入选了10人名单,求甲成为参赛选手的概率;
![]() 设抽取的3名选手中女生的人数为
设抽取的3名选手中女生的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附表: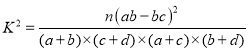 ,其中
,其中![]() .
.
| 0.010 | 0.05 | 0.001 |
| 6.635 | 7.879 | 10.828 |
【答案】(1)列联表见解析,没有99%以上的把握认为智力游戏水平高低与性别有关,
(2)![]()
![]() ,
,![]() 分布列见解析,
分布列见解析,![]()
【解析】
(1)根据题意完善![]() 列联表,再计算
列联表,再计算![]() ,对照临界值得出结论即可.
,对照临界值得出结论即可.
(2)![]() 从
从![]() 人中抽取
人中抽取![]() 人共有
人共有![]() 个基本事件,甲为参赛选手共有
个基本事件,甲为参赛选手共有![]() 个基本事件,再利代入古典概型公式即可.
个基本事件,再利代入古典概型公式即可.![]() 首先用分层抽样得到抽取的男、女生人数,得到女生的人数
首先用分层抽样得到抽取的男、女生人数,得到女生的人数![]() 的所有取值为0,1,2,3,计算出相应的概率,再列出分布列,计算数学期望即可.
的所有取值为0,1,2,3,计算出相应的概率,再列出分布列,计算数学期望即可.
(1)
性别 | 高级 | 非高级 | 合计 |
女 | 40 | 160 | 200 |
男 | 60 | 140 | 200 |
合计 | 100 | 300 | 400 |
![]() ,所以没有99%以上的把握认为智力游戏水平高低与性别有关
,所以没有99%以上的把握认为智力游戏水平高低与性别有关
(2)![]() 甲入选3人名单的概率为
甲入选3人名单的概率为![]() ;
;
![]() 根据分层抽样的特征10人中男女各5人,女生的人数
根据分层抽样的特征10人中男女各5人,女生的人数![]() 的所有取值为0,1,2,3;
的所有取值为0,1,2,3;
![]() ,
,![]() ,
,
![]() ,
,![]() ;
;
所以![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
期望![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,
,![]() 为平面内一动点,以线段
为平面内一动点,以线段![]() 为直径的圆内切于圆
为直径的圆内切于圆![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的标准方程;
的标准方程;
(2)已知过坐标原点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,若在曲线
两点,若在曲线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求
,求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行,求
轴平行,求![]() ;
;
(2)已知![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)写出![]() 所有可能的零点个数及相应的
所有可能的零点个数及相应的![]() 的取值范围.(请直接写出结论)
的取值范围.(请直接写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2017年起,全国各省市陆续实施了新高考,许多省市采用了“![]() ”的选科模式,即:考生除必考的语数外三科外,再从物理化学生物历史地理政治六个学科中,任意选取三科参加高考,为了调查新高考中考生的选科情况,某地调查小组对某中学进行了一次调查,研究考生选择化学与选择物理是否有关.已知在调查数据中,选物理的考生与不选物理的考生人数相同,其中选物理且选化学的人数占选物理人数的
”的选科模式,即:考生除必考的语数外三科外,再从物理化学生物历史地理政治六个学科中,任意选取三科参加高考,为了调查新高考中考生的选科情况,某地调查小组对某中学进行了一次调查,研究考生选择化学与选择物理是否有关.已知在调查数据中,选物理的考生与不选物理的考生人数相同,其中选物理且选化学的人数占选物理人数的![]() ,在不选物理的考生中,选化学与不选化学的人数比为
,在不选物理的考生中,选化学与不选化学的人数比为![]() .
.
(1)若在此次调查中,选物理未选化学的考生有100人,将选物理且选化学的人数占选化学总人数的比作为概率,从该中学选化学的考生中随机抽取4人,记这4人中选物理且选择化学的考生人数为![]() ,求
,求![]() 的分布列(用排列数组合数表示即可)和数学期望.
的分布列(用排列数组合数表示即可)和数学期望.
(2)若研究得到在犯错误概率不超过0.01的前提下,认为选化学与选物理有关,则选物理且选化学的人数至少有多少?(单位:百人,精确到0.01)
附: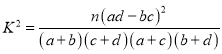 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
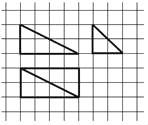
【题目】我国古代数学名著《九章算术商功》中阐述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,对该几何体有如下描述:
①四个侧面都是直角三角形;
②最长的侧棱长为![]() ;
;
③四个侧面中有三个侧面是全等的直角三角形;
④外接球的表面积为24π.
其中正确的描述为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(1+x)t﹣1的定义域为(﹣1,+∞),其中实数t满足t≠0且t≠1.直线l:y=g(x)是f(x)的图象在x=0处的切线.
(1)求l的方程:y=g(x);
(2)若f(x)≥g(x)恒成立,试确定t的取值范围;
(3)若a1,a2∈(0,1),求证: ![]() .注:当α为实数时,有求导公式(xα)′=αxα﹣1.
.注:当α为实数时,有求导公式(xα)′=αxα﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了拓展城市的旅游业,实现不同市区间的物资交流,政府决定在![]() 市与
市与![]() 市之间建一条直达公路,中间设有至少8个的偶数个十字路口,记为
市之间建一条直达公路,中间设有至少8个的偶数个十字路口,记为![]() ,现规划在每个路口处种植一颗杨树或者木棉树,且种植每种树木的概率均为
,现规划在每个路口处种植一颗杨树或者木棉树,且种植每种树木的概率均为![]() .
.
(1)现征求两市居民的种植意见,看看哪一种植物更受欢迎,得到的数据如下所示:
A市居民 | B市居民 | |
喜欢杨树 | 300 | 200 |
喜欢木棉树 | 250 | 250 |
是否有![]() 的把握认为喜欢树木的种类与居民所在的城市具有相关性;
的把握认为喜欢树木的种类与居民所在的城市具有相关性;
(2)若从所有的路口中随机抽取4个路口,恰有![]() 个路口种植杨树,求
个路口种植杨树,求![]() 的分布列以及数学期望;
的分布列以及数学期望;
(3)在所有的路口种植完成后,选取3个种植同一种树的路口,记总的选取方法数为![]() ,求证:
,求证:![]() .
.
附: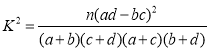
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com