
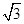 ,求l的方程;
,求l的方程;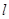 的方程为:
的方程为: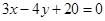 或
或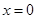 (2)
(2)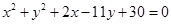
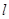 的距离为2 当直线的斜率存在时,设所求直线
的距离为2 当直线的斜率存在时,设所求直线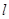 的方程为:
的方程为: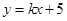 即
即 由点到直线的距离公式即可求出k的值,从而得直线
由点到直线的距离公式即可求出k的值,从而得直线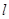 的方程 然后再考虑斜率不存在时的情况 (2)设过点P的圆C的弦的中点为
的方程 然后再考虑斜率不存在时的情况 (2)设过点P的圆C的弦的中点为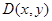 ,则
,则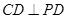 即
即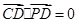 由此等式即可得中点D的轨迹方程 这属于利用等量关系求轨迹方程的问题
由此等式即可得中点D的轨迹方程 这属于利用等量关系求轨迹方程的问题 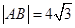 ,设
,设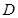 是线段
是线段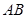 的中点,则
的中点,则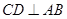
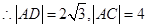 点C的坐标为(-2,6) 在
点C的坐标为(-2,6) 在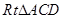 中,可得
中,可得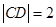
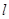 的方程为:
的方程为: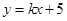 即
即
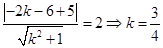
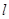 的方程为:
的方程为: 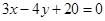 4分
4分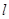 的斜率不存在时,也满足题意,此时方程为:
的斜率不存在时,也满足题意,此时方程为: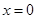
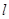 的方程为:
的方程为: 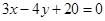 或
或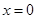 6分
6分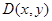 ,则
,则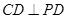 即
即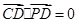
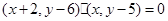 化简得所求轨迹的方程为:
化简得所求轨迹的方程为: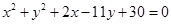 12分
12分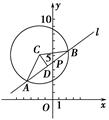


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com