
【题目】已知![]() 为实数,函数
为实数,函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)求函数![]() 在
在![]() 上的最小值
上的最小值![]() ;
;
(Ⅲ)若![]() ,求使方程
,求使方程![]() 有唯一解的
有唯一解的![]() 的值.
的值.
【答案】(Ⅰ)当![]() 时,递增区间为
时,递增区间为![]() ;当
;当![]() 时,递减区间为
时,递减区间为![]() ,递增区间为
,递增区间为![]() ; (Ⅱ)
; (Ⅱ)![]() ; (Ⅲ)
; (Ⅲ)![]() .
.
【解析】
(Ⅰ)首先求出函数![]() 定义域与
定义域与![]() ,然后根据
,然后根据![]() 与0的大小关系,分类讨论,即可求得函数
与0的大小关系,分类讨论,即可求得函数![]() 的单调区间;
的单调区间;
(Ⅱ)根据(Ⅰ),分![]() 和
和![]() 讨论函数
讨论函数![]() 的单调性,从而根据函数单调性求得
的单调性,从而根据函数单调性求得![]() 的最小值;
的最小值;
(Ⅲ)设![]() ,然后将问题转化为
,然后将问题转化为![]() 有唯一解,从而通过求导研究函数
有唯一解,从而通过求导研究函数![]() 的单调性得到
的单调性得到![]() ,进而构造新函数,通过研究新函数的单调性求得
,进而构造新函数,通过研究新函数的单调性求得![]() 的值.
的值.
(Ⅰ)由题意,函数![]() ,
,
可得![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,令
时,令![]() ,解得
,解得![]() ;令
;令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(Ⅱ)由(Ⅰ)可知,
①当![]() 时,
时,![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() ;
;
②当![]() 时,
时,![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
若![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() ;若
;若![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上增函数,
上增函数,
所以![]() ,
,
综上可得![]() .
.
(Ⅲ)若方程![]() 有唯一解,设
有唯一解,设![]() 有唯一解,
有唯一解,
令![]() ,可得
,可得![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() 或
或![]() (舍去),
(舍去),
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是单调递减函数;
上是单调递减函数;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是单调递增函数,
上是单调递增函数,
所以当![]() 时,函数取得最小值,最小值为
时,函数取得最小值,最小值为![]() ,
,
因为![]() 有唯一解,所以
有唯一解,所以![]() ,
,
所以 ,即
,即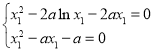 ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
设函数![]() ,∵
,∵![]() 时,
时,![]() 是增函数,
是增函数,
所以![]() 至多有一个解,且
至多有一个解,且![]() ,
,
所以方程![]() 得解为
得解为![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以当![]() 时,方程
时,方程![]() 有唯一解时
有唯一解时![]() 的值为
的值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是![]() ,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,曲线C经过伸缩变换
,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,曲线C经过伸缩变换 得到曲线E,直线
得到曲线E,直线 (t为参数)与曲线E交于A,B两点.
(t为参数)与曲线E交于A,B两点.
(1)设曲线C上任一点为![]() ,求
,求![]() 的最小值;
的最小值;
(2)求出曲线E的直角坐标方程,并求出直线l被曲线E截得的弦AB长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点的坐标为
的右焦点的坐标为![]() ,且长轴长为短轴长的
,且长轴长为短轴长的![]() 倍.椭圆
倍.椭圆![]() 的上、下顶点分别为
的上、下顶点分别为![]() ,经过点
,经过点![]() 的直线
的直线![]() 与椭圆相交于
与椭圆相交于![]() 两点(不同于
两点(不同于![]() 两点).
两点).
(1)求椭圆的方程;
(2)若直线![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)设直线![]() 相交于点
相交于点![]() ,求证:
,求证:![]() 是定值.
是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部门在上班高峰时段对甲、乙两座地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,单位:分钟)将统计数据按![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分组,制成频率分布直方图如图所示:
分组,制成频率分布直方图如图所示:


(1)求a的值;
(2)记A表示事件“在上班高峰时段某乘客在甲站乘车等待时间少于20分钟”试估计A的概率;
(3)假设同组中的每个数据用该组区间左端点值来估计,记在上班高峰时段甲、乙两站各抽取的50名乘客乘车的平均等待时间分别为![]() ,求
,求![]() 的值,并直接写出
的值,并直接写出![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 右顶点与上顶点,坐标原点
右顶点与上顶点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且点
,且点![]() 是圆
是圆![]() 的圆心,动直线
的圆心,动直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 在线段
在线段![]() 上,
上,![]() ,且当
,且当![]() 取最小值时直线
取最小值时直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的值;
的值;
(3)若直线![]() 与圆
与圆![]() 分别交于
分别交于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 上,且
上,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高尔顿(钉)板是在一块竖起的木板上钉上一排排互相平行、水平间隔相等的圆柱形铁钉(如图),并且每一排钉子数目都比上一排多一个,一排中各个钉子恰好对准上面一排两相邻铁钉的正中央.从入口处放入一个直径略小于两颗钉子间隔的小球,当小球从两钉之间的间隙下落时,由于碰到下一排铁钉,它将以相等的可能性向左或向右落下,接着小球再通过两铁钉的间隙,又碰到下一排铁钉.如此继续下去,在最底层的5个出口处各放置一个容器接住小球.

(Ⅰ)理论上,小球落入4号容器的概率是多少?
(Ⅱ)一数学兴趣小组取3个小球进行试验,设其中落入4号容器的小球个数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代的四书是指:《大学》、《中庸》、《论语》、《孟子》,甲、乙、丙、丁![]() 名同学从中各选一书进行研读,已知四人选取的书恰好互不相同,且甲没有选《中庸》,乙和丙都没有选《论语》,则
名同学从中各选一书进行研读,已知四人选取的书恰好互不相同,且甲没有选《中庸》,乙和丙都没有选《论语》,则![]() 名同学所有可能的选择有______种.
名同学所有可能的选择有______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蜂巢是由工蜂分泌蜂蜡建成的.从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成.如图,在正六棱柱![]() 的三个顶点
的三个顶点![]() 处分别用平面
处分别用平面![]() ,平面
,平面![]() ,平面
,平面![]() 截掉三个相等的三棱锥
截掉三个相等的三棱锥![]() ,
,![]() ,
,![]() ,平面
,平面![]() ,平面
,平面![]() ,平面
,平面![]() 交于点
交于点![]() ,就形成了蜂巢的结构,如下图(4)所示,
,就形成了蜂巢的结构,如下图(4)所示,
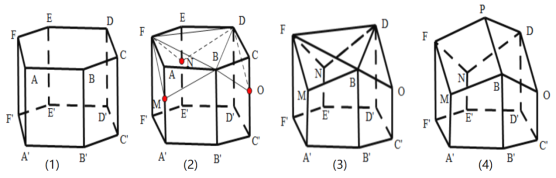
瑞士数学家克尼格利用微积分的方法证明了蜂巢的这种结构是在相同容积下所用材料最省的,英国数学家麦克劳林通过计算得到菱形的一个内角为![]() ,即
,即![]() .以下三个结论①
.以下三个结论①![]() ;②
;② ![]()
![]()
![]() ;③
;③![]() 四点共面,正确命题的个数为______个;若
四点共面,正确命题的个数为______个;若![]() ,
,![]() ,
,![]() ,则此蜂巢的表面积为_______.
,则此蜂巢的表面积为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,2),B为抛物线x2=2y﹣2上任意一点,且B为AC的中点,设动点C的轨迹为曲线E.
(1)求曲线E的方程;
(2)是否存在斜率为1的直线l交曲线E于M、N两点,使得△MAN为以MN为底边的等腰三角形?若存在,请求出l的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com