
(本题满分13分)
函数 是定义在
是定义在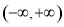 上的奇函数,且
上的奇函数,且 。
。
(1)求实数a,b,并确定函数 的解析式;
的解析式;
(2)判断 在(-1,1)上的单调性,并用定义证明你的结论;
在(-1,1)上的单调性,并用定义证明你的结论;
(3)写出 的单调减区间,并判断
的单调减区间,并判断 有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
(1)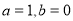 ,
,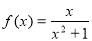 ;
;
(2) 在(-1,1)上是增函数;
(3) 单调减区间为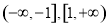 ,
,
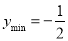 ,
,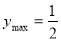 .
.
【解析】
试题分析:(1)先根据函数为奇函数(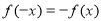 )求出
)求出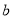 值,再利用
值,再利用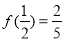 求出
求出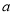 值,即可其解析式;(2)利用函数的单调性定义进行判定与证明;(3)结合(2)问容易得到单调递减区间,进而写出最值.
值,即可其解析式;(2)利用函数的单调性定义进行判定与证明;(3)结合(2)问容易得到单调递减区间,进而写出最值.
解题思路:(1)求解析式的一种主要方法是待定系数法;(2)利用函数单调性的定义证明函数的单调性的一般步骤为:设值代值、作差变形、判定符号、下结论.
试题解析:(1) 是奇函数,
是奇函数,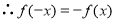 。
。
即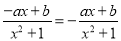 ,
,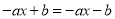 ,
,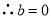
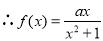 ,又
,又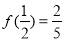 ,
, ,
,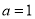 ,
,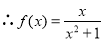
(2)任取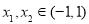 ,且
,且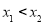 ,
,
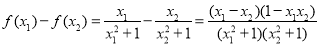
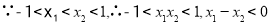 ,
,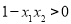
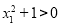 ,
, ,
,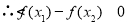 ,
,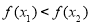 ,
,
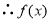 在(-1,1)上是增函数。
在(-1,1)上是增函数。
(3)单调减区间为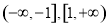
当x=-1时,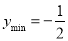 ,当x=1时,
,当x=1时,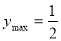 .
.
考点:1.函数的奇偶性;2.函数的解析式;3.函数的单调性与最值.


科目:高中数学 来源:2014-2015学年山东省高一上学期10月月考数学试卷(解析版) 题型:选择题
函数f(x)=  ,则f(-3)=( )
,则f(-3)=( )
A.-6 B .6 C.-12 D.12
查看答案和解析>>
科目:高中数学 来源:2014-2015学年安徽省铜陵市高二上学期第一次月考数学试卷(解析版) 题型:填空题
两圆x2+y2-4x+6y=0和x2+y2-6x=0的连心线方程为___________
查看答案和解析>>
科目:高中数学 来源:2014-2015学年安徽省高二10月月考文科数学试卷(解析版) 题型:填空题
一段细绳长10cm,把它拉直后随机剪成两段,则两段长度都超过4的概率为__________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com