Question

已知ABCD是矩形，PD=DC=a,AD=a,PD⊥平面ABCD，M、N分别是AD、PB的中点.

(1)求证：平面MNC⊥平面PBC；

(2)求点A到平面MNC的距离.

Answer 1

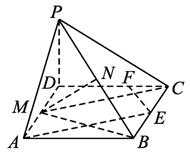
(方法一)证明：(1)连结PM，BM，PM==,

BM==,∴PM=BM,∴MN⊥PB,

    又有：PC==a,

∴BC=PC,∴CN⊥PB,∴PB⊥平面MNC，∴平面MNC⊥平面PBC；

(2)取BC中点，NC中点，

    易证得：AE∥MC，

    故点A到平面MNC的距离就是点E到平面MNC的距离.

    因PB⊥平面MNC，∴EF∥PB，

    故EF⊥平面MNC，故点E到平面MNC的距离就是EF.

    因EF=,因PB==2a,

    故EF=.

    故点A到平面MNC的距离是.

(方法二)

(1)如图，建立空间直角坐标系D—XYZ，则：

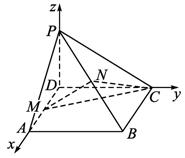
P(0,0,a),B(a,a,0),M(,0,0),C(0,a,0),N(,,).

=(0,,), =(,-,),=(a,a,-a)

∴⊥,⊥.

∴PB⊥平面MNC，

∴平面PBC⊥平面MNC.

(2)由上可知：⊥，

    设点A到平面MNC的距离为h，易知点N到平面ACM的距离为,

    且：||=,||=a,故有：S_△MNC=||·||=,又S_△AMC=||·||=,

    因V_A—MNC=V_N—AMC，故有：h=,

    即点A到平面MNC的距离是.