
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角).以原点为极点,
的倾斜角).以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,并在两个坐标系下取相同的长度单位.
轴的非负半轴为极轴建立极坐标系,并在两个坐标系下取相同的长度单位.
(1)当![]() 时,求直线
时,求直线![]() 的极坐标方程;
的极坐标方程;
(2)若曲线![]() 和直线
和直线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图象关于直线
,其图象关于直线![]() 对称,为了得到函数
对称,为了得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上的所有点( )
的图象上的所有点( )
A.先向左平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
B.先向右平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
C.先向右平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
D.先向左平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:①函数![]() ;
;
②向量![]() ,
,![]() ,且
,且![]() ,
,![]() ;
;
③函数![]() 的图象经过点
的图象经过点![]()
请在上述三个条件中任选一个,补充在下面问题中,并解答.
已知_________________,且函数![]() 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)求函数![]() 在
在![]() 上的单调递减区间.
上的单调递减区间.
注:如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆台O1O2的轴截面为等腰梯形A1A2B2B1,A1A2![]() B1B2,A1A2=2B1B2,A1B1=2,圆台O1O2的侧面积为6π.若点C,D分别为圆O1,O2上的动点且点C,D在平面A1A2B2B1的同侧.
B1B2,A1A2=2B1B2,A1B1=2,圆台O1O2的侧面积为6π.若点C,D分别为圆O1,O2上的动点且点C,D在平面A1A2B2B1的同侧.
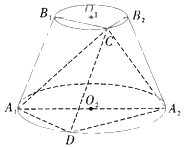
(1)求证:A1C⊥A2C;
(2)若∠B1B2C=60°,则当三棱锥C﹣A1DA2的体积取最大值时,求A1D与平面CA1A2所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|2x+4|+|x-3|.
(1)解关于x的不等式f(x)<8;
(2)对于正实数a,b,函数g(x)=f(x)-3a-4b只有一个零点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 是线段
是线段![]() 的中点,直线
的中点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年,山东省高考将全面实行“
年,山东省高考将全面实行“![]() 选
选![]() ”的模式(即:语文、数学、外语为必考科目,剩下的物理、化学、历史、地理、生物、政治六科任选三科进行考试).为了了解学生对物理学科的喜好程度,某高中从高一年级学生中随机抽取
”的模式(即:语文、数学、外语为必考科目,剩下的物理、化学、历史、地理、生物、政治六科任选三科进行考试).为了了解学生对物理学科的喜好程度,某高中从高一年级学生中随机抽取![]() 人做调查.统计显示,男生喜欢物理的有
人做调查.统计显示,男生喜欢物理的有![]() 人,不喜欢物理的有
人,不喜欢物理的有![]() 人;女生喜欢物理的有
人;女生喜欢物理的有![]() 人,不喜欢物理的有
人,不喜欢物理的有![]() 人.
人.
(1)据此资料判断是否有![]() 的把握认为“喜欢物理与性别有关”;
的把握认为“喜欢物理与性别有关”;
(2)为了了解学生对选科的认识,年级决定召开学生座谈会.现从![]() 名男同学和
名男同学和![]() 名女同学(其中
名女同学(其中![]() 男
男![]() 女喜欢物理)中,选取
女喜欢物理)中,选取![]() 名男同学和
名男同学和![]() 名女同学参加座谈会,记参加座谈会的
名女同学参加座谈会,记参加座谈会的![]() 人中喜欢物理的人数为
人中喜欢物理的人数为![]() ,求
,求![]() 的分布列及期望
的分布列及期望![]() .
.
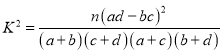 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“金镶玉”是北京奥运会的奖牌设计所采用的式样,喻示中国传统文化中的“金玉良缘”,体现了中国人对奥林匹克精神的礼赞和对运动员的褒奖.它的设计方案,创意十分新颖,突破了以往任何一届奥运会奖牌设计单一材质的传统,又融入了典型的中国文化元素,是中国文化与体育精神完美结合的载体.现有一矩形玉片![]() ,
,![]() 为
为![]() 毫米,
毫米,![]() 为32毫米,
为32毫米,![]() 为
为![]() 的中点.现要开槽镶嵌金丝,将其加工为镶金工艺品,如图,金丝部分为优弧
的中点.现要开槽镶嵌金丝,将其加工为镶金工艺品,如图,金丝部分为优弧![]() 和线段
和线段![]() 其中优弧
其中优弧![]() 所在圆的圆心为
所在圆的圆心为![]() ,圆
,圆![]() 与矩形的边
与矩形的边![]() 分别相切于点
分别相切于点![]() 以及点
以及点![]() 在线段
在线段![]() 上(
上(![]() 在
在![]() 的左侧),
的左侧),![]() 分别于圆
分别于圆![]() 相切于点
相切于点![]() 且
且![]() .若优弧
.若优弧![]() 部分镶嵌的金丝每毫米造价为
部分镶嵌的金丝每毫米造价为![]() 元(
元(![]() ),线段
),线段![]() 部分镶嵌的金丝每毫米造价为
部分镶嵌的金丝每毫米造价为![]() 元.记锐角
元.记锐角![]() 镶嵌金丝的总造价为
镶嵌金丝的总造价为![]() 元.
元.
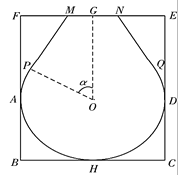
(1)试表示出关于![]() 的函数
的函数![]() 并写出
并写出![]() 的范围;
的范围;
(2)当镶嵌金丝的总造价最低时,求出四边形![]() 的面积
的面积![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com