

思路解析:由l被l1、l2截得线段长为3![]() ,又l1、l2间的距离为3,可求得l与l2的夹角为45°,由夹角公式可求l的斜率,从而得解.
,又l1、l2间的距离为3,可求得l与l2的夹角为45°,由夹角公式可求l的斜率,从而得解.
解:设直线l的方程为y-3=k(x-2),即kx-y+3-2k=0.
设l与l1交于点M,作MN⊥l2于点N(如图7-3-8).
两平行线l1、l2间距离|MN|=![]() =3.
=3.
在Rt△MNQ中,|MQ|=3![]() ,sin∠MQN=
,sin∠MQN=![]() =
=![]() ,∴∠MQN=45°,即直线l与l2的夹角是45°.于是tan45°=
,∴∠MQN=45°,即直线l与l2的夹角是45°.于是tan45°=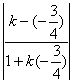 .解之,得k=
.解之,得k=![]() 或k=-7.
或k=-7.
∴所求直线方程为x-7y+19=0或7x+y-17=0.
深化升华
本题构造一个Rt△MNQ,求l2与l的夹角,进而求出所求直线的斜率,从而求出直线l的方程.本题如采用解方程组的方法求交点M(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),再利用|MQ|=3
),再利用|MQ|=3![]() 来解出k,运算很繁杂,比较之下,本题用前一类解法好.
来解出k,运算很繁杂,比较之下,本题用前一类解法好.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
|
|
| π |
| 2 |
| π |
| 4 |
| a2+b2 |
| c2+d2 |
| (ac+bd)(ad+bc) |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•乐山一模)如图,已知直线l过点A(0,4),交函数y=2x的图象于点C,交x轴于点B,若AC:CB=2:3,则点B的横坐标为
(2013•乐山一模)如图,已知直线l过点A(0,4),交函数y=2x的图象于点C,交x轴于点B,若AC:CB=2:3,则点B的横坐标为查看答案和解析>>
科目:高中数学 来源:2013年四川省乐山市高考数学一模试卷(理科)(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com