
已知二次函数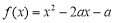 (
(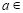 R).
R).
(1)解不等式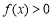 ;
;
(2)函数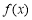 在
在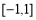 上有零点,求
上有零点,求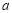 的取值范围.
的取值范围.
(1) 时,解集为R;
时,解集为R;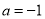 或
或 时,解集为
时,解集为 ;
;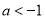 或
或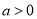 时,解集为
时,解集为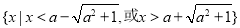 ;(2)
;(2)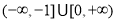 。
。
【解析】
试题分析:(1)这是一道含参数一元二次不等式问题,因为判别式含有参数 ,需要对
,需要对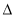 进行分类讨论;
进行分类讨论;
(2)思路一:函数 在
在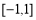 上有零点,即函数
上有零点,即函数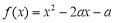 图像在区间
图像在区间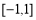 上与
上与 轴有交点,然后就交点的个数分类讨论。思路二:函数
轴有交点,然后就交点的个数分类讨论。思路二:函数 在
在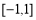 上有零点,即方程
上有零点,即方程
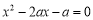 有根,可化为
有根,可化为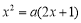 ,然后对
,然后对 进行讨论,
进行讨论, 不为零时,可化为
不为零时,可化为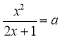 ,然后构造函数
,然后构造函数 ,转化为求该函数在
,转化为求该函数在 上的最值问题。
上的最值问题。
试题解析:(1)方程 的判别式
的判别式 ,
,
当 时,
时, ,不等式
,不等式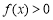 的解集为R;
的解集为R;
当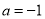 或
或 时,
时,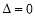 ,不等式
,不等式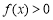 的解集为
的解集为 ;
;
当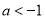 或
或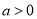 时,
时, ,
,
不等式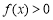 的解集为
的解集为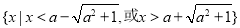 . 6分
. 6分
(2)法1:当 时,
时, 在
在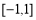 上有一个零点0;
上有一个零点0;
当 时,
时, 在
在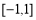 上有一个零点-1;
上有一个零点-1;
当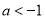 时,考虑到
时,考虑到 ,对称轴
,对称轴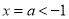 ,则有
,则有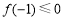 ,得
,得 ,
,
所以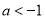 ;
;
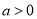 时,考虑到
时,考虑到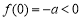 ,对称轴
,对称轴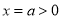 ,则有
,则有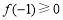 ,得
,得 ,
,
所以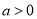 .
.
综上,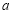 的取值范围为
的取值范围为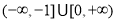 . 16分
. 16分
法2:由 ,得
,得 ①,
①,
对于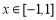 ,
,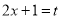 ,则
,则 ,
, ,变为
,变为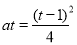 ②
②
若 ,则②不成立,故可得
,则②不成立,故可得 ,
,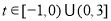 .
.
令 ,则
,则 .
.
当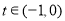 时,
时, ,
,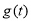 单调递减;当
单调递减;当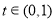 时,
时, ,
,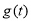 单调递减;
单调递减;
当 时,
时,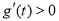 ,
,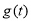 单调递增.所以
单调递增.所以 的值域为
的值域为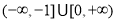 .
.
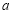 的取值范围为
的取值范围为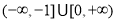 . 16分
. 16分
考点:(1)含参数一元二次不等式的解法;(2)一元二次方程根的分布问题;(3)构造函数及分类讨论思想的应用。


科目:高中数学 来源:2015届江西省南昌市三校高三10月联考理科数学试卷(解析版) 题型:选择题
已知 ,
, 是不共线的向量,若
是不共线的向量,若 =λ
=λ +
+ ,
, =
= +μ
+μ (λ,μ∈R),则A, B, C三点共线的充要条件是:( )
(λ,μ∈R),则A, B, C三点共线的充要条件是:( )
A.λ+μ=1 B.λ-μ=1 C.λμ=1 D.λμ=-1
查看答案和解析>>
科目:高中数学 来源:2015届江苏省连云港高二下学期期末数学试卷(选修物理)(解析版) 题型:填空题
将1、2、3、4、5、6、7、8、9这9个正整数分别写在三张卡片上,要求每一张卡片上的三个数字中任意两数之差都不在这张卡片上.现在第一张卡片上已经写有1和5,第二张卡片上写有2,第三张卡片上写有3,则第一张卡片上的另外一个数字是 .
查看答案和解析>>
科目:高中数学 来源:2015届江苏省苏州市高三上学期期中测试数学试卷(解析版) 题型:解答题
(本题满分14分)已知向量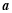
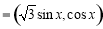 ,
,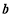
 ,
,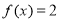
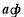
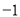 .
.
(1)求函数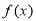 的单调递减区间及其图象的对称轴方程;
的单调递减区间及其图象的对称轴方程;
(2)当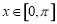 时,若
时,若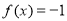 ,求
,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com