
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线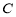 的参数方程为
的参数方程为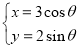 (
(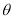 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线 上的点按坐标变换
上的点按坐标变换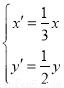 得到曲线
得到曲线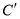 .
.
(1)求曲线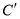 的普通方程;
的普通方程;
(2)若点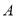 在曲线
在曲线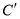 上,点
上,点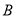
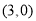 ,当点
,当点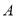 在曲线
在曲线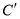 上运动时,求
上运动时,求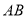 中点
中点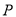 的轨迹方程.
的轨迹方程.
(1) ;(2)
;(2)
【解析】
试题分析:(1)将参数方程转化为直角坐标系下的普通方程,需要根据参数方程的结构特征,选取恰当的消参方法,常见的消参方法有:代入消参法、加减消参法、平方消参法;(2)将参数方程转化为普通方程时,要注意两种方程的等价性,不要增解、漏解,若 有范围限制,要标出
有范围限制,要标出 的取值范围;(3)直角坐标方程化为极坐标方程,只需把公式
的取值范围;(3)直角坐标方程化为极坐标方程,只需把公式 及
及 直接代入并化简即可;而极坐标方程化为极坐标方程要通过变形,构造形如
直接代入并化简即可;而极坐标方程化为极坐标方程要通过变形,构造形如 ,
, ,
, 的形式,进行整体代换,其中方程的两边同乘以(或同除以)
的形式,进行整体代换,其中方程的两边同乘以(或同除以) 及方程的两边平方是常用的变形方法.
及方程的两边平方是常用的变形方法.
试题解析:(1) :
:

 ,
,
将

 代入
代入 的普通方程得
的普通方程得 ,即
,即 ;
;
(2)设

 , 则
, 则
所以 ,即
,即
代入 ,得
,得 ,即
,即
 中点
中点 的轨迹方程为
的轨迹方程为 .
.
考点:1、参数方程与普通方程的互化;2、点的轨迹方程.
考点分析: 考点1:参数方程 试题属性

科目:高中数学 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试理科数学试卷(解析版) 题型:选择题
若框图所给的程序运行结果为 ,那么判断框中应填入的关于
,那么判断框中应填入的关于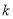 的条件是( )
的条件是( )
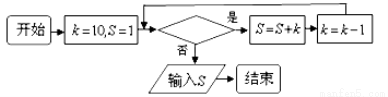
A.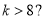 B.
B.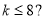 C.
C.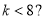 D.
D.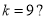
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省龙岩市非一级达标校高三上学期期末检查理科数学试卷(解析版) 题型:选择题
下列结论正确的是( )
A.命题“若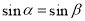 ,则
,则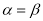 ”是真命题
”是真命题
B.若函数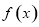 可导,且在
可导,且在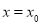 处有极值,则
处有极值,则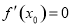
C.向量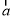 ,
,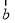 的夹角为钝角的充要条件是
的夹角为钝角的充要条件是
D.命题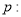 “
“ ,
,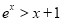 ”的否定是“
”的否定是“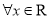 ,
,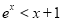 ”
”
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南省弥勒市高三年级模拟测试一文科数学试卷(解析版) 题型:解答题
(本小题满分12分)某校从参加某次知识竞赛的同学中,选取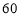 名同学将其成绩(百分制,均为整数)分成
名同学将其成绩(百分制,均为整数)分成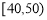 ,
,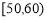 ,
,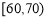 ,
,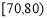 ,
,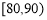 ,
,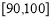 六组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.
六组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.
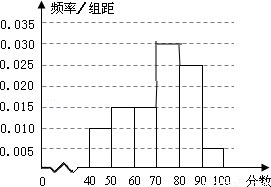
(1)从频率分布直方图中,估计本次考试成绩的中位数;
(2)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南省弥勒市高三年级模拟测试一文科数学试卷(解析版) 题型:选择题
三棱锥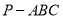 中,
中,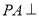 平面
平面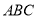 ,
, ,则该三棱锥外接球的表面积为( )
,则该三棱锥外接球的表面积为( )
A.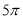 B.
B.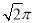 C.
C. D.
D.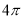
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南省弥勒市高三年级模拟测试一理科数学试卷(解析版) 题型:解答题
(本小题满分12分)某市规定,高中学生三年在校期间参加不少于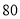 小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段
小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段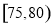 ,
,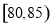 ,
,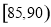 ,
,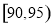 ,
,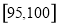 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.

(1)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;
(2)从全市高中学生(人数很多)中任意选取3位学生,记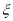 为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量
为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量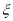 的分布列和数学期望
的分布列和数学期望 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市奉贤区高三上学期期末调研测试数学试卷(解析版) 题型:解答题
设 是定义在
是定义在 上的函数,若对任何实数
上的函数,若对任何实数 以及
以及 中的任意两数
中的任意两数 、
、 ,恒有
,恒有 ,则称
,则称 为定义在
为定义在 上的
上的 函数.
函数.
(1)证明函数 是定义域上的
是定义域上的 函数;
函数;
(2)判断函数 是否为定义域上的
是否为定义域上的 函数,请说明理由;
函数,请说明理由;
(3)若 是定义域为
是定义域为 的函数,且最小正周期为
的函数,且最小正周期为 ,试证明
,试证明 不是
不是 上的
上的 函数.
函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com