
△ABC的内角A、B、C的对边分别为a,b,c,asin A+csin C- asin C=bsin B.
asin C=bsin B.
(1)求B;
(2)若A=75°,b=2,求a,c.
(1) B=45°. (2) a=1+ ,c=
,c=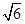 .
.
解析试题分析: (1)由正弦定理得a2+c2- ac=b2. (2分)
ac=b2. (2分)
由余弦定理得b2=a2+c2-2accos B. (4分)
故cos B=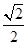 ,又0°<B<180°,因此B=45°. (6分)
,又0°<B<180°,因此B=45°. (6分)
(2)sin A=sin(30°+45°)=sin 30°cos 45°+cos 30°sin 45°=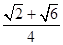 .(8分)
.(8分)
故a=b· =
=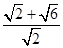 =1+
=1+ ,(10分)
,(10分)
c=b·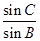 =2·
=2·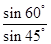 =
=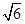 .(12分)
.(12分)
考点:本题主要考查正弦定理、余弦定理的应用,两角和与差的三角函数。
点评:典型题,本题解答思路明确,首先应用正弦定理,转化得到边的关系式,利用余弦定理求角。(2)应用正弦定理及两角和与差的三角函数公式,确定边长。本题较易。


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:解答题
如图,甲船以每小时 海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 的方向
的方向 处,此时两船相距20海里.当甲船航行20分钟到达
处,此时两船相距20海里.当甲船航行20分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com