
分析 (1)先求函数导数,再讨论参数范围确定导数符号即可.
(2)由条件得到不等关系,再进行整体换元转化为一元不等式的证明问题
解答 解:(1)g(x)=lnx+ax2-(2a+1)x,
g′(x)=$\frac{1}{x}$+2ax-(2a+1)=$\frac{2a(x-\frac{1}{2a})(x-1)}{x}$,(x>0),
∴①当$\frac{1}{2a}$<1,即a>$\frac{1}{2}$时,令g'(x)>0得,0<x<$\frac{1}{2a}$或x>1;
令g'(x)<0得,$\frac{1}{2a}$<x<1.
所以,增区间为(0,$\frac{1}{2a}$),(1,+∞);减区间为($\frac{1}{2a}$,1);
②当$\frac{1}{2a}$>1,即0<a<$\frac{1}{2}$时,令g'(x)>0得,0<x<1或x>$\frac{1}{2a}$;
令g'(x)<0得,$\frac{1}{2a}$<x<1.
所以,增区间为(0,1),($\frac{1}{2a}$,+∞);减区间为($\frac{1}{2a}$,1);
③当$\frac{1}{2a}$=1,即a=$\frac{1}{2}$时,g′(x)=$\frac{{(x-1)}^{2}}{x}$>0,增区间为(0,+∞).
综上,当0<a<$\frac{1}{2}$时,增区间为(0,1),($\frac{1}{2a}$,+∞);减区间为(1,$\frac{1}{2a}$);
当a=$\frac{1}{2}$时,增区间为(0,+∞);
当a>$\frac{1}{2}$时,增区间为(0,$\frac{1}{2a}$),(1,+∞);减区间为($\frac{1}{2a}$,1).
(2)证明:依题,k=$\frac{l{nx}_{2}-l{nx}_{1}}{{{x}_{2}-x}_{1}}$,要证$\frac{1}{{x}_{2}}$<k<$\frac{1}{{x}_{1}}$,
只要证 $\frac{1}{{x}_{2}}$<$\frac{l{nx}_{2}-l{nx}_{1}}{{{x}_{2}-x}_{1}}$<$\frac{1}{{x}_{1}}$,
因为 x2-x1>0,故只要证$\frac{{x}_{2}{-x}_{1}}{{x}_{2}}$<ln $\frac{{x}_{2}}{{x}_{1}}$<$\frac{{x}_{2}{-x}_{1}}{{x}_{1}}$,
令$\frac{{x}_{2}}{{x}_{1}}$=t(t>1),则只需证 1-$\frac{1}{t}$<lnt<t-1(t>1),
令h(t)=lnt+$\frac{1}{t}$-1(t>1),则h′(t)=$\frac{1}{t}$-$\frac{1}{{t}^{2}}$=$\frac{t-1}{{t}^{2}}$>0,
∴h(t)在(1,+∞)上单调递增,
∴h(t)>h(1)=0,即lnt>1-$\frac{1}{t}$(t>1),
同理可证:lnt<t-1,
综上,1-$\frac{1}{t}$<lnt<t-1(t>1),即$\frac{1}{{x}_{2}}$<k<$\frac{1}{{x}_{1}}$.
点评 本题考查了导数的几何意义和导数在函数中的运用.考查了逻辑思维和运算能力以及转化的思想方法.属于难题.


科目:高中数学 来源: 题型:选择题
| A. | p真q假 | B. | p 假q真 | C. | p真q真 | D. | p 假q假 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
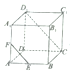 如图,在正方体中ABCD-A1B1C1D1,E、F分别为AB,AA1的中点.求证:
如图,在正方体中ABCD-A1B1C1D1,E、F分别为AB,AA1的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知空间四边形OABC,如图所示,其对角线为OB、AC,M、N分别为OA、BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=3$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x•$\overrightarrow{OA}$+y•$\overrightarrow{OB}$+z•$\overrightarrow{OC}$,则x、y、z的和为$\frac{7}{8}$.
已知空间四边形OABC,如图所示,其对角线为OB、AC,M、N分别为OA、BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=3$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x•$\overrightarrow{OA}$+y•$\overrightarrow{OB}$+z•$\overrightarrow{OC}$,则x、y、z的和为$\frac{7}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{e}$,$\frac{1}{\sqrt{e}}$) | B. | (-$\frac{1}{\sqrt{e}}$,$\sqrt{e}$) | C. | (-∞,$\sqrt{e}$) | D. | (-∞,$\frac{1}{\sqrt{e}}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{5π}{21}$,0) | B. | ($\frac{π}{21}$,0) | C. | ($\frac{π}{42}$,0) | D. | (0,$\frac{\sqrt{3}}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com