
 已知空间四边形OABC,如图所示,其对角线为OB、AC,M、N分别为OA、BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=3$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x•$\overrightarrow{OA}$+y•$\overrightarrow{OB}$+z•$\overrightarrow{OC}$,则x、y、z的和为$\frac{7}{8}$.
已知空间四边形OABC,如图所示,其对角线为OB、AC,M、N分别为OA、BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=3$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x•$\overrightarrow{OA}$+y•$\overrightarrow{OB}$+z•$\overrightarrow{OC}$,则x、y、z的和为$\frac{7}{8}$. 分析 利用向量的三角形法则及平行四边形法则和向量形式的中点公式即可得出.
解答 解:∵空间四边形OABC对角线为OB、AC,M、N分别为OA、BC的中点,
点G在线段MN上,且$\overrightarrow{MG}$=3$\overrightarrow{GN}$,
∴$\overrightarrow{OG}$=$\overrightarrow{OM}+\overrightarrow{MG}$=$\overrightarrow{OM}$+$\frac{3}{4}$$\overrightarrow{MN}$
=$\overrightarrow{OM}+\frac{3}{4}(\overrightarrow{ON}-\overrightarrow{OM})$
=$\frac{1}{4}\overrightarrow{OM}+\frac{3}{4}\overrightarrow{ON}$
=$\frac{1}{4}×\frac{1}{2}\overrightarrow{OA}$+$\frac{3}{4}×\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})$
=$\frac{1}{8}\overrightarrow{OA}+\frac{3}{8}\overrightarrow{OB}+\frac{3}{8}\overrightarrow{OC}$,
∵$\overrightarrow{OG}$=x•$\overrightarrow{OA}$+y•$\overrightarrow{OB}$+z•$\overrightarrow{OC}$,
∴x+y+z=$\frac{1}{8}+\frac{3}{8}+\frac{3}{8}$=$\frac{7}{8}$.
故答案为:$\frac{7}{8}$.
点评 本题考查三个数的和的求法,是基础题,解题时要认真审题,注意平面向量加法法则的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
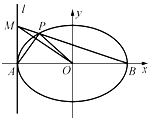 如图,在平面直角坐标系xOy中,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且经过点$(2,\sqrt{6})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.
如图,在平面直角坐标系xOy中,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且经过点$(2,\sqrt{6})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
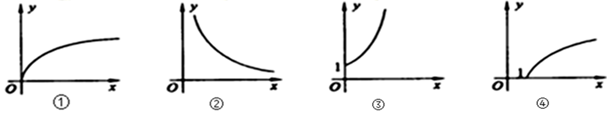
| A. | ②①③④ | B. | ②③①④ | C. | ④①③② | D. | ④③①② |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
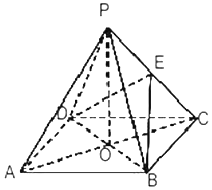 如图,ABCD是正方形,O是该正方体的中心,P是平面ABCD外一点,PO⊥平面ABCD,E是PC的中点.
如图,ABCD是正方形,O是该正方体的中心,P是平面ABCD外一点,PO⊥平面ABCD,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com