
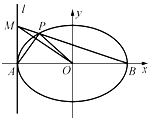
 如图,在平面直角坐标系xOy中,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且经过点$(2,\sqrt{6})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.
如图,在平面直角坐标系xOy中,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且经过点$(2,\sqrt{6})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.分析 (1)根据离心率和点在椭圆上,列方程解得即可,
(2)设直线BM的斜率为k,直线BM的方程为:y=k(x-4),设P(x1,y1),与椭圆方程联立可得(2k2+1)x2-16k2x+32k2-16=0,解得x1,x2.可得P坐标,由y=k(x-4),解得M(-4,-4k),只要证明AP•OM=0,即可得出.
(3)利用数量积运算即可得出是否为定值.
解答 解:(1)∵椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且经过点$(2,\sqrt{6})$,
∴e2=1-$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{2}$,$\frac{4}{{a}^{2}}$+$\frac{6}{{b}^{2}}$=1,
解得a2=16,b2=8
∴$\frac{x^2}{16}+\frac{y^2}{8}=1$,
(2)由(1)知,A(-4,0),B(4,0),直线BM斜率显然存在,
设BM方程为y=k(x-4),则M(-4,-8k),设P(x1,y2),
由$\left\{\begin{array}{l}{y=k(x-4)}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{8}=1}\end{array}\right.$,得(2k2+1)x2-16k2x+32k2-16=0,△>0,
解得x1=$\frac{8{k}^{2}-4}{1+2{k}^{2}}$,x2=4,
y1=$\frac{-8k}{1+2{k}^{2}}$,
∴P($\frac{8{k}^{2}-4}{1+2{k}^{2}}$,$\frac{-8k}{1+2{k}^{2}}$),
∴$\overrightarrow{AP}$=($\frac{16{k}^{2}}{1+2{k}^{2}}$,$\frac{-8k}{1+2{k}^{2}}$),$\overrightarrow{OM}$=(-4,-8k),
∴$\overrightarrow{AP}$•$\overrightarrow{OM}$=$\frac{16{k}^{2}}{1+2{k}^{2}}$×(-4)+$\frac{-8k}{1+2{k}^{2}}$×(-8k)=0,
∴AP⊥OM.
(3)∵$\overrightarrow{OP}$=($\frac{8{k}^{2}-4}{1+2{k}^{2}}$,$\frac{-8k}{1+2{k}^{2}}$),
∴$\overrightarrow{OP}$•$\overrightarrow{OM}$=$\frac{8{k}^{2}-4}{1+2{k}^{2}}$×(-4)+$\frac{-8k}{1+2{k}^{2}}$×(-8k)=$\frac{16(1+2{k}^{2})}{1+2{k}^{2}}$=16
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到交点坐标、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当-2<a<2时,函数f(x)无极值 | B. | 当a>2时,f(x)的极小值小于0 | ||
| C. | 当a=2时,x=1是f(x)的一个极值点 | D. | ?a∈R,f(x)必有零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等于$\frac{{\sqrt{3}}}{2}$ | B. | 等于$-\frac{{\sqrt{3}}}{2}$ | C. | 等于$±\frac{{\sqrt{3}}}{2}$ | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知空间四边形OABC,如图所示,其对角线为OB、AC,M、N分别为OA、BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=3$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x•$\overrightarrow{OA}$+y•$\overrightarrow{OB}$+z•$\overrightarrow{OC}$,则x、y、z的和为$\frac{7}{8}$.
已知空间四边形OABC,如图所示,其对角线为OB、AC,M、N分别为OA、BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=3$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x•$\overrightarrow{OA}$+y•$\overrightarrow{OB}$+z•$\overrightarrow{OC}$,则x、y、z的和为$\frac{7}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,将两块三角板拼在一起组成一个平面四边形ABCD,若$\overrightarrow{AC}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$(x,y∈R).则x+y=1+$\frac{4\sqrt{3}}{3}$.
如图,将两块三角板拼在一起组成一个平面四边形ABCD,若$\overrightarrow{AC}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$(x,y∈R).则x+y=1+$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com