
| A. | 当-2<a<2时,函数f(x)无极值 | B. | 当a>2时,f(x)的极小值小于0 | ||
| C. | 当a=2时,x=1是f(x)的一个极值点 | D. | ?a∈R,f(x)必有零点 |
分析 根据函数的单调性以及a的范围分别对各个选项进行判断即可.
解答 解:(1)f(x)的定义域是(0,+∞),
f′(x)=$\frac{1}{x}$+x-a≥2-a,
故-2<a<2时,f′(x)>0,
f(x)在(0,+∞)递增,函数无极值,
故A正确;
(2)a>2时,f′(x)=$\frac{{x}^{2}-ax+1}{x}$,
令g(x)=x2-ax+1,△=a2-4>0,
x1=$\frac{a-\sqrt{{a}^{2}-4}}{2}$>0,x2=$\frac{a+\sqrt{{a}^{2}-4}}{2}$,
故f(x)在(0,$\frac{a-\sqrt{{a}^{2}-4}}{2}$)递增,在$\frac{a-\sqrt{{a}^{2}-4}}{2}$,$\frac{a+\sqrt{{a}^{2}-4}}{2}$)递减,在($\frac{a+\sqrt{{a}^{2}-4}}{2}$,+∞)递增;
故f(x)的极小值是f($\frac{a+\sqrt{{a}^{2}-4}}{2}$)=ln$\frac{a+\sqrt{{a}^{2}-4}}{2}$-$\frac{{a}^{2}}{4}$-$\frac{a\sqrt{{a}^{2}-4}}{4}$+$\frac{1}{2}$<lna-$\frac{{a}^{2}}{2}$+$\frac{1}{2}$,
令h(a)=lna-$\frac{{a}^{2}}{2}$+$\frac{1}{2}$,(a>2),h′(a)=$\frac{1}{a}$-a<0,
故h(a)在(2,+∞)递减,h(a)<h(2)=ln2-$\frac{3}{2}$<0,
故a>2时,f(x)的极小值小于0,
故B正确;
(3)a=2时,f(x)=lnx+$\frac{1}{2}$x2-2x+1,
f′(x)=$\frac{{(x-1)}^{2}}{x}$≥0,f(x)递增,无极值点,
故C错误;
(4)x→0时,f(x)→-∞,
x→+∞时,f(x)→+∞,
显然f(x)有零点,
故D正确;
故选;C.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 空间几何体ABCDEF如图所示.已知面ABCD⊥面ADEF,ABCD为梯形,ADEF为正方形,且AB∥CD,AB⊥AD,CD=4,AB=AD=2,G为CE的中点.
空间几何体ABCDEF如图所示.已知面ABCD⊥面ADEF,ABCD为梯形,ADEF为正方形,且AB∥CD,AB⊥AD,CD=4,AB=AD=2,G为CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
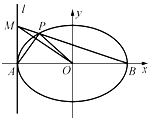 如图,在平面直角坐标系xOy中,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且经过点$(2,\sqrt{6})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.
如图,在平面直角坐标系xOy中,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且经过点$(2,\sqrt{6})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
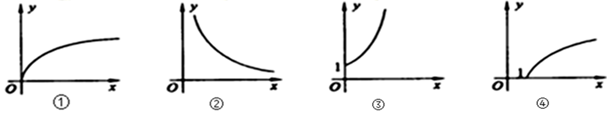
| A. | ②①③④ | B. | ②③①④ | C. | ④①③② | D. | ④③①② |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
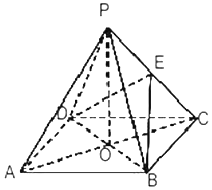 如图,ABCD是正方形,O是该正方体的中心,P是平面ABCD外一点,PO⊥平面ABCD,E是PC的中点.
如图,ABCD是正方形,O是该正方体的中心,P是平面ABCD外一点,PO⊥平面ABCD,E是PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com