
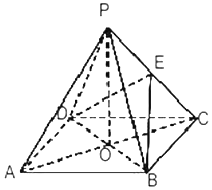
 如图,ABCD是正方形,O是该正方体的中心,P是平面ABCD外一点,PO⊥平面ABCD,E是PC的中点.
如图,ABCD是正方形,O是该正方体的中心,P是平面ABCD外一点,PO⊥平面ABCD,E是PC的中点.分析 (1)要证PA与平面EBD平行,而过PA的平面PAC与平面EBD的交线为EO,因此只要证PA∥EO即可,这可由中位线定理得证;
(2)要证BD垂直于平面PAC,就是要证BD与平面PAC内两条相交直线垂直,正方形中对角线BD与AC是垂直的,因此只要再证BD⊥PO,这由线面垂直的性质或定义可得.
解答 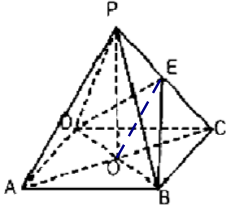 证明:(1)连接EO,∵四边形ABCD为正方形,
证明:(1)连接EO,∵四边形ABCD为正方形,
∴O为AC的中点,
∵E是PC的中点,∴OE是△APC的中位线.
∴EO∥PA,∵EO?平面BDE,PA?平面BDE,
∴PA∥平面BDE.
(2)∵PO⊥平面ABCD,BD?平面ABCD,
∴PO⊥BD,
∵四边形ABCD是正方形,
∴AC⊥BD,
∵PO∩AC=O,AC?平面PAC,PO?平面PAC,
∴BD⊥平面PAC.
点评 本题考查线面平行、线面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | 当-2<a<2时,函数f(x)无极值 | B. | 当a>2时,f(x)的极小值小于0 | ||
| C. | 当a=2时,x=1是f(x)的一个极值点 | D. | ?a∈R,f(x)必有零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知空间四边形OABC,如图所示,其对角线为OB、AC,M、N分别为OA、BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=3$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x•$\overrightarrow{OA}$+y•$\overrightarrow{OB}$+z•$\overrightarrow{OC}$,则x、y、z的和为$\frac{7}{8}$.
已知空间四边形OABC,如图所示,其对角线为OB、AC,M、N分别为OA、BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=3$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x•$\overrightarrow{OA}$+y•$\overrightarrow{OB}$+z•$\overrightarrow{OC}$,则x、y、z的和为$\frac{7}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{e}$,$\frac{1}{\sqrt{e}}$) | B. | (-$\frac{1}{\sqrt{e}}$,$\sqrt{e}$) | C. | (-∞,$\sqrt{e}$) | D. | (-∞,$\frac{1}{\sqrt{e}}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{5π}{21}$,0) | B. | ($\frac{π}{21}$,0) | C. | ($\frac{π}{42}$,0) | D. | (0,$\frac{\sqrt{3}}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,将两块三角板拼在一起组成一个平面四边形ABCD,若$\overrightarrow{AC}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$(x,y∈R).则x+y=1+$\frac{4\sqrt{3}}{3}$.
如图,将两块三角板拼在一起组成一个平面四边形ABCD,若$\overrightarrow{AC}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$(x,y∈R).则x+y=1+$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{18}$个长度单位 | B. | 向右左平移$\frac{π}{18}$个长度单位 | ||
| C. | 向左平移$\frac{π}{9}$个长度单位 | D. | 向右左平移$\frac{π}{9}$个长度单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 8 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com