
分析 ①画出函数的图形,即可得到解的个数;
②由题意,方程f(x)=ax恰有两个不同实数根,等价于y=f(x)与y=ax有2个交点,又a表示直线y=ax的斜率,求出a的取值范围.
解答 解:①函数$f(x)=\left\{\begin{array}{l}\frac{1}{4}x+1,\;x≤1\\ lnx,x>1\end{array}\right.$,
与y=-x的图象如图: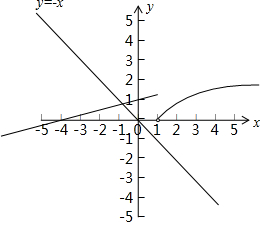
可知方程f(x)=-x有1个根.
②函数$f(x)=\left\{\begin{array}{l}\frac{1}{4}x+1,\;x≤1\\ lnx,x>1\end{array}\right.$,
∵方程f(x)=ax恰有两个不同实数根,
∴y=f(x)与y=ax有2个交点,
又∵a表示直线y=ax的斜率,
∴y′=$\frac{1}{x}$,
设切点为(x0,y0),k=$\frac{1}{{x}_{0}}$,
∴切线方程为y-y0=$\frac{1}{{x}_{0}}$(x-x0),
而切线过原点,∴y0=1,x0=e,k=$\frac{1}{e}$,
∴直线l1的斜率为$\frac{1}{e}$,
又∵直线l2与y=$\frac{1}{4}$x+1平行,
∴直线l2的斜率为$\frac{1}{4}$,
∴实数a的取值范围是[$\frac{1}{4}$,$\frac{1}{e}$)
故答案为:①1,②$[\frac{1}{4},\frac{1}{e})$.
点评 本题考查了函数的图象与性质的应用问题,函数的导数的应用,考查函数与方程的关系,是易错题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{x}{2017x+1}$ | B. | $\frac{x}{x+2017}$ | C. | $\frac{2017x}{2017x+1}$ | D. | $\frac{2017x+1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 空间几何体ABCDEF如图所示.已知面ABCD⊥面ADEF,ABCD为梯形,ADEF为正方形,且AB∥CD,AB⊥AD,CD=4,AB=AD=2,G为CE的中点.
空间几何体ABCDEF如图所示.已知面ABCD⊥面ADEF,ABCD为梯形,ADEF为正方形,且AB∥CD,AB⊥AD,CD=4,AB=AD=2,G为CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2k+1 | B. | 2(2k+1) | C. | $\frac{2k+1}{k+1}$ | D. | $\frac{2k+2}{k+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2016) | B. | (-2018,-2016) | C. | (-2016,-2) | D. | (-2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
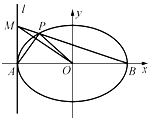 如图,在平面直角坐标系xOy中,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且经过点$(2,\sqrt{6})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.
如图,在平面直角坐标系xOy中,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且经过点$(2,\sqrt{6})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com