
分析 (1)利用等差数列与等比数列的通项公式即可得出.
(2)利用等差数列与等比数列的求和公式即可得出.
解答 解:(1)设等差数列{an}的公差为d,依题意得a5=a1+4d⇒3+4d=15⇒d=3,所以an=3+3(n-1)=3n.
设等比数列{cn}的公比为q,依题意得c1=b1-a1=4-3=1,c5=b5-a5=31-15=16,
从而${c_5}={c_1}{q^4}⇒16=1×{q^4}⇒q=2$,所以${c_n}=1×{2^{n-1}}={2^{n-1}}$.
(2)因为${c_n}={b_n}-{a_n}⇒{b_n}={a_n}+{c_n}⇒{b_n}=3n+{2^{n-1}}$,所以数列{bn}的前n项和Sn=(3+1)+(6+2)+(9+22)+…+(3n+2n-1)
=(3+6+…+3n)+(1+2+22+…+2n-1)
=$\frac{n(3+3n)}{2}$+$\frac{{2}^{n}-1}{2-1}$
=$\frac{3{n}^{2}+3n}{2}$+2n-1.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、分组求和方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2016) | B. | (-2018,-2016) | C. | (-2016,-2) | D. | (-2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
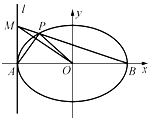 如图,在平面直角坐标系xOy中,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且经过点$(2,\sqrt{6})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.
如图,在平面直角坐标系xOy中,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且经过点$(2,\sqrt{6})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
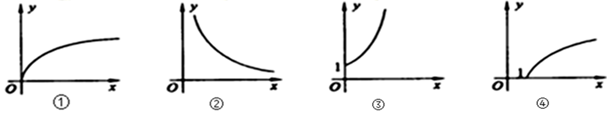
| A. | ②①③④ | B. | ②③①④ | C. | ④①③② | D. | ④③①② |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com