
分析 由条件利用三角函数的单调性,求得各个函数的单调区间.
解答 解:(1)对于y=$\sqrt{3}$sin($\frac{2π}{5}$x-$\frac{π}{3}$),令2kπ-$\frac{π}{2}$≤$\frac{2π}{5}$x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,
求得5k-$\frac{5}{12}$≤x≤5k+$\frac{25}{12}$,k∈Z,故函数的增区间为[5k-$\frac{5}{12}$,5k+$\frac{25}{12}$],k∈Z;
令2kπ+$\frac{π}{2}$≤$\frac{2π}{5}$x-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,求得5k+$\frac{25}{12}$≤x≤5k+$\frac{55}{12}$,k∈Z,故函数的减区间为[5k+$\frac{25}{12}$,5k+$\frac{55}{12}$],k∈Z.
(2)对于y=4sin($\frac{π}{3}$-$\frac{3}{4}$x)=-4sin($\frac{3}{4}$x-$\frac{π}{3}$),令2kπ-$\frac{π}{2}$≤$\frac{3x}{4}$-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,
求得$\frac{8}{3}$kπ-$\frac{2π}{9}$≤x≤$\frac{8}{3}$kπ+$\frac{5π}{9}$,k∈Z,故函数的减区间为[$\frac{8}{3}$kπ-$\frac{2π}{9}$,$\frac{8}{3}$kπ+$\frac{5π}{9}$],k∈Z;
令2kπ+$\frac{π}{2}$≤$\frac{3x}{4}$-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,求得$\frac{8}{3}$kπ+$\frac{5π}{9}$≤x≤$\frac{8}{3}$kπ+$\frac{22π}{9}$,k∈Z,故函数的增区间为[$\frac{8}{3}$kπ+$\frac{5π}{9}$,$\frac{8}{3}$kπ+$\frac{22π}{9}$],k∈Z.
(3)对于y=$\frac{1}{2}$cos(3x+$\frac{π}{4}$),令2kπ-π≤3x+$\frac{π}{4}$≤2kπ,
求得 $\frac{2}{3}$kπ-$\frac{5π}{12}$≤x≤$\frac{2}{3}$k-$\frac{π}{12}$,k∈Z,故函数的增区间为[$\frac{2}{3}$kπ-$\frac{5π}{12}$,$\frac{2}{3}$k-$\frac{π}{12}$],k∈Z;
令2kπ≤3x+$\frac{π}{4}$≤2kπ+π,求得$\frac{2}{3}$kπ-$\frac{π}{12}$≤x≤$\frac{2}{3}$kπ+$\frac{π}{4}$,k∈Z,故函数的减区间为[$\frac{2}{3}$kπ+$\frac{π}{12}$,$\frac{2}{3}$kπ+$\frac{π}{4}$],k∈Z.
(4)对于y=3tan($\frac{1}{2}$x-$\frac{2}{3}$π),令kπ-$\frac{π}{2}$<$\frac{1}{2}$x-$\frac{2π}{3}$<kπ+$\frac{π}{2}$,
求得2k+$\frac{π}{3}$<x<2k+$\frac{7π}{3}$,k∈Z,故函数的增区间为(2k+$\frac{π}{3}$,2k+$\frac{7π}{3}$),k∈Z.
点评 本题主要考查三角函数的单调性,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+ln2}{2}$ | B. | $\frac{1+2ln2}{4}$ | C. | $\frac{1-ln2}{2}$ | D. | $\frac{3-2ln2}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|1≤x≤2} | C. | {x|1≤x<2} | D. | {x|0≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
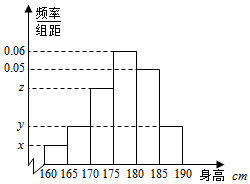 为了了解某中学男生身高,从该校的总共800名男生中抽取40名进行调查,并制成如下频率分布直方图,已知x:y:z=1:2:4.则y的值为0.02.
为了了解某中学男生身高,从该校的总共800名男生中抽取40名进行调查,并制成如下频率分布直方图,已知x:y:z=1:2:4.则y的值为0.02.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 102 | B. | 114 | C. | 126 | D. | 138 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 90 | B. | 180 | C. | 360 | D. | 405 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com