练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

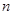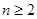    一个口袋中装有2个白球和个红球（且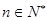），每次从袋中摸出两个球（每次摸球后把这两个球放回袋中），若摸出的两个球颜色相同为中奖，否则为不中奖．
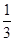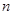    (Ⅰ) 摸球一次，若中奖概率为，求的值；
    (Ⅱ) 若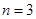，摸球三次，记中奖的次数为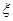，试写出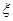的分布列并求其期望．

    (Ⅰ)；(Ⅱ)．

    解析试题分析：(Ⅰ)由古典概率的求法，可求出；(Ⅱ)摸球三次，中奖情况可能为;0,1,2,3次，分别求出概率，得分布列从而求出期望．
    试题解析：（1）；
    （2）若，则每次摸球中奖的概率
    因此，，分布列如下：


    		0
    		1
    		2
    		3
    P




    ．
    考点：1、古典概率的求法，2、分布列与期望的求法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    如图，从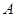到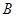有6条网线，数字表示该网线单位时间内可以通过的最大信息量，现从中任取3条网线且使每条网线通过最大信息量，设这三条网线通过的最大信息之和为.

    （1）当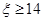时，线路信息畅通，求线路信息畅通的概率；
    （2）求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    有一种密码，明文是由三个字符组成，密码是由明文对应的五个数字组成，编码规则如下表：明文由表中每一排取一个字符组成且第一排取的字符放在第一位，第二排取的字符放在第二位，第三排取的字符放在第三位，对应的密码由明文对应的数字按相同的次序排列组成．

    第一排
    		明文字符
    		A
    		B
    		C
    		D
    密码字符
    		11
    		12
    		13
    		14
    第二排
    		明文字符
    		E
    		F
    		G
    		H
    密码字符
    		21
    		22
    		23
    		24
    第三排
    		明文字符
    		M
    		N
    		P
    		Q
    密码字符
    		1
    		2
    		3
    		4
    设随机变量ξ表示密码中不同数字的个数．
    (1)求；
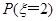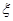    (2)求随机变量的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

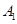    在某次模块水平测试中，某同学对于政治、历史、地理这三个学科每个学科是否能达到优秀水平的概率都为，记政治、历史、地理达到优秀水平的事件分别为、、，未达到优秀水平的事件分别为、、．
    （Ⅰ）若将事件 “该同学这三科中恰有两科达到优秀水平” 记为，试求事件发生的概率；
    （Ⅱ）请依据题干信息，仿照（Ⅰ）的叙述，设计一个关于该同学测试成绩情况的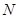事件，使得事件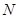发生的概率大于，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某同学参加省学业水平测试，物理、化学、生物获得等级和获得等级不是的机会相等，物理、化学、生物获得等级的事件分别记为、、，物理、化学、生物获得等级不是的事件分别记为、、.
    （Ⅰ）试列举该同学这次水平测试中物理、化学、生物成绩是否为的所有可能结果（如三科成绩均为记为）；
    （Ⅱ）求该同学参加这次水平测试获得两个的概率；
    （Ⅲ）试设计一个关于该同学参加这次水平测试物理、化学、生物成绩情况的事件，使该事件的概率大于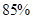，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    为调查乘客的候车情况，公交公司在某站台的60名候车乘客中随机抽取15人，将他们的候车时间（单位：分钟）作为样本分成5组，如下表所示：
    （1）估计这60名乘客中候车时间少于10分钟的人数；
    （2）若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查，求抽到的两人恰好来自不同组的概率．

    组别
    		候车时间
    		人数
    一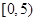
    		 
    		2
    二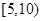

    		6
    三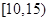

    		4
    四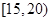

    		2
    五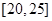

    		1
     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本小题满分12分）有一种密码，明文是由三个字符组成，密码是由明文对应的五个数字组成，编码规则如下表：明文由表中每一排取一个字符组成，且第一排取的字符放在第一位，第二排取的字符放在第二位，第三排取的字符放在第三位，对应的密码由明文对应的数字按相同的次序排成一排组成.

     
    第一排
    		明文字符
    		A
    		B
    		C
    		D
    密码字符
    		11
    		12
    		13
    		14
     
    第二排
    		明文字符
    		E
    		F
    		G
    		H
    密码字符
    		21
    		22
    		23
    		24
     
    第三排
    		明文字符
    		M
    		N
    		P
    		Q
    密码字符
    		1
    		2
    		3
    		4
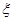    设随机变量表示密码中不同数字的个数．
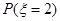    (Ⅰ)求；   (Ⅱ)求随机变量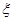的分布列和它的数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    选聘高校毕业生到村任职，是党中央作出的一项重大决策，这对培养社会主义新农村建设带头人、引导高校毕业生面向基层就业创业，具有重大意义。为了响应国家号召，某大学决定从符合条件的6名（其中男生4人，女生2人）报名大学生中选择3人，到某村参加村委会主任应聘考核。
    （Ⅰ）设所选3人中女生人数为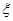，求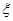的分布列及数学期望；
    （Ⅱ）在男生甲被选中的情况下，求女生乙也被选中的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    甲、乙、丙三人进行羽毛球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判，设各局中双方获胜的概率均为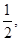各局比赛的结果都相互独立，第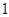局甲当裁判.
    （I）求第局甲当裁判的概率；
    （II）求前局中乙恰好当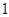次裁判概率.

    查看答案和解析>>

    同步练习册答案