
【题目】已知全集U={x|x2﹣3x+2≥0},A={x||x﹣2|>1},B= ![]()
求:
(1)A∩B;
(2)A∩UB;
(3)U(A∪B).
【答案】
(1)解:由U=x|x2﹣3x+2≥0
化简得:U={x|x≤1或x≥2}
由A=x||x﹣2|>1
化简得:A={x|x<1或x>3}
由B= ![]()
化简得:B={x|x<1或x>2}
A∩B={x|x<1或x>3}
(2)解:CUB={1,2}
A∩CUB=
(3)解:A∪B={x|x<1或x>2}
CU(A∪B)={1,2}
【解析】根据 ![]() ,分别进行化简,然后①直接求A∩B,②先求CUB再求A∩CUB,③先求A∪B,再求CU(A∪B.
,分别进行化简,然后①直接求A∩B,②先求CUB再求A∩CUB,③先求A∪B,再求CU(A∪B.
【考点精析】掌握集合的并集运算和集合的交集运算是解答本题的根本,需要知道并集的性质:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,则A
=A,A∪B=B∪A;(2)若A∪B=B,则A![]() B,反之也成立;交集的性质:(1)A∩B
B,反之也成立;交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立.
B,反之也成立.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】如图,一条河的两岸平行,河的宽度d=600m,一艘客船从码头A出发匀速驶往河对岸的码头B.已知|AB|=1km,水流速度为2km/h, 若客船行驶完航程所用最短时间为6分钟,则客船在静水中的速度大小为( )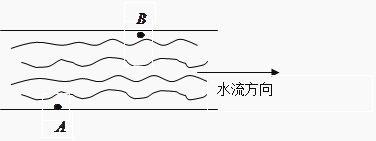
A.8km/h
B.![]() km/h
km/h
C.![]() km/h
km/h
D.10km/h
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知直线l的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为![]() 。
。
(Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点A(0,1),B(0,﹣1),C(1,0),动点P满足: ![]() ,
,
(1)求动点P的轨迹方程,并说明方程表示的曲线类型;
(2)当k=2,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论,其中正确的个数为( ). ①已 ![]() ,则
,则 ![]()
②过原点作曲线 ![]() 的切线,则切线方程为
的切线,则切线方程为 ![]() (其中e为自然对数的底数);
(其中e为自然对数的底数);
③已知随机变 ![]()
![]() ,则
,则 ![]()
④已知n为正偶数,用数学归纳法证明等式 ![]() 时,若假设
时,若假设 ![]() 时,命题为真,则还需利用归纳假设再证明
时,命题为真,则还需利用归纳假设再证明 ![]() 时等式成立,即可证明等式对一切正偶数n都成立.
时等式成立,即可证明等式对一切正偶数n都成立.
⑤在回归分析中,常用 ![]() 来刻画回归效果,在线性回归模型中,
来刻画回归效果,在线性回归模型中, ![]() 表示解释变量对于预报变量变化的贡献率
表示解释变量对于预报变量变化的贡献率 ![]() 越接近1,表示回归的效果越好.
越接近1,表示回归的效果越好.
A.2
B.3
C.4
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com