练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    曲线f (x)= x3+x－2在P0点处的切线平行于直线y= 4x－1，则P0点的坐标为 （   ）

           A．（1，0）                                             B．（2，8）

           C．（1，0）和（－1，－4）                     D．（2，8）和（－1，－4）

     

    【答案】

    C

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2013•潍坊一模）设函数f(x)=
    1
    3
    mx3+(4+m)x2，g(x)=alnx    ，其中a≠0．
    （ I ）若函数y=g（x）图象恒过定点P，且点P在y=f（x）的图象上，求m的值；
    （Ⅱ）当a=8时，设F（x）=f′（x）+g（x），讨论F（x）的单调性；
    （Ⅲ）在（I）的条件下，设G(x)=
    f(x)，x≤1
    g(x)，x＞1
    ，曲线y=G（x）上是否存在两点P、Q，使△OPQ（O为原点）是以O为直角顶点的直角三角形，且该三角形斜边的中点在y轴上？如果存在，求a的取值范围；如果不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：湖南省衡阳市八中2011届高三第二次月考文科数学试题 题型：013

    曲线f(x)＝x·1nx在点x＝1处的切线方程为

    [　　]
    A．

    y＝2x－2

    B．

    y＝2x＋2

    C．

    y＝x－1

    D．

    y＝x＋1

    查看答案和解析>>

    科目：高中数学 来源：潍坊一模 题型：解答题

    设函数f(x)=
    1
    3
    mx3+(4+m)x2，g(x)=alnx    ，其中a≠0．
    （ I ）若函数y=g（x）图象恒过定点P，且点P在y=f（x）的图象上，求m的值；
    （Ⅱ）当a=8时，设F（x）=f′（x）+g（x），讨论F（x）的单调性；
    （Ⅲ）在（I）的条件下，设G(x)=
    f(x)，x≤1
    g(x)，x＞1
    ，曲线y=G（x）上是否存在两点P、Q，使△OPQ（O为原点）是以O为直角顶点的直角三角形，且该三角形斜边的中点在y轴上？如果存在，求a的取值范围；如果不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

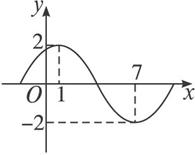
    已知正弦曲线f(x)=Asin(ωx+φ)(A＞0,ω＞0,0＜φ＜π)的一部分图象如图所示.

    (1)求函数f(x)的解析式;

    (2)求证:x=1是y=f(x)的对称轴;

    (3)求y=f(x)关于x=2对称的图象y=g(x)的解析式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (理)已知函数f(x)=xlnx.

    (1)求函数f(x)的单调区间和最小值;

    (2)当b＞0时，求证:bb≥(其中e=2.718 28…是自然对数的底数);

    (3)若a＞0,b＞0，证明f(a)+(a+b)ln2≥f(a+b)-f(b).

    (文)已知向量m=(x2,y-cx),n=(1,x+b)(x,y,b,c∈R)且m∥n,把其中x,y所满足的关系式记为y=f(x).若f′(x)为f(x)的导函数,F(x)=f(x)+af′(x)(a＞0),且F(x)是R上的奇函数.

    (1)求和c的值.

    (2)求函数f(x)的单调递减区间(用字母a表示).

    (3)当a=2时,设0＜t＜4且t≠2,曲线y=f(x)在点A(t,f(t))处的切线与曲线y=f(x)相交于点B(m,f(m))(A与B不重合),直线x=t与y=f(m)相交于点C,△ABC的面积为S,试用t表示△ABC的面积S(t),并求S(t)的最大值.

    查看答案和解析>>

    同步练习册答案