
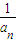 }��ǰn��ĺ�ΪTn������{Tn}��ǰn��ĺ�ΪRn����֤����n��2ʱ��Rn-1=n��Tn-1��
}��ǰn��ĺ�ΪTn������{Tn}��ǰn��ĺ�ΪRn����֤����n��2ʱ��Rn-1=n��Tn-1��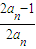 }��ǰn������Ƿ����ʵ��a��ʹ�ò���ʽAn
}��ǰn������Ƿ����ʵ��a��ʹ�ò���ʽAn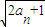 ��a��һ��n��N+�������������ڣ����a��ȡֵ��Χ���������ڣ���˵�����ɣ�
��a��һ��n��N+�������������ڣ����a��ȡֵ��Χ���������ڣ���˵�����ɣ�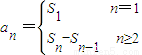 �����an����2�ʾ���Ҫ����ѧ���ɷ�֤��������֤��n=2ʱ��ʽ�������ټ��� n=kʱ��ʽ��������n=k+1ʱ������������Ҫ���úü���������Rk=Rk-1+Tk�Ϳ�֤������3��д��An�ı���ʽ����
�����an����2�ʾ���Ҫ����ѧ���ɷ�֤��������֤��n=2ʱ��ʽ�������ټ��� n=kʱ��ʽ��������n=k+1ʱ������������Ҫ���úü���������Rk=Rk-1+Tk�Ϳ�֤������3��д��An�ı���ʽ����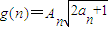 �������������n�ĺ�������ΪAn��һ��n��ij˻������Բ������̵ķ����жϳ�g��n���ĵ����ԣ��Ӷ�ʹ����ʽ�õ�֤����
�������������n�ĺ�������ΪAn��һ��n��ij˻������Բ������̵ķ����жϳ�g��n���ĵ����ԣ��Ӷ�ʹ����ʽ�õ�֤����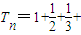
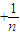 ��Rn=T1+T2+T3+��+Tn��
��Rn=T1+T2+T3+��+Tn��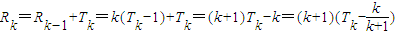 =
=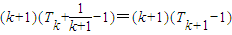 ��
��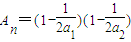 ��
��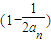 ����
����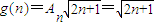
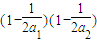 ��
��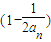 ��
��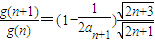 =
=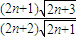 ��1
��1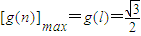
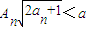 ��һ��n��N+������ֻ��
��һ��n��N+������ֻ��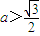 ���ɣ�
���ɣ�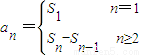 ���֪ʶ�㣮��2����Ҫ��������ѧ���ɷ�֤�����ؼ����� n=k+1ʱ���Ƶ�����Ҫ���úü����������������������ļ����Խ�ǿ����3���DZ�����ѵ����ڣ���Ϊ�����жϵ����Եķ�����������̱Ƚ����ã������ɱ�����ص�����������һ����Ҫһ����˼ά����
���֪ʶ�㣮��2����Ҫ��������ѧ���ɷ�֤�����ؼ����� n=k+1ʱ���Ƶ�����Ҫ���úü����������������������ļ����Խ�ǿ����3���DZ�����ѵ����ڣ���Ϊ�����жϵ����Եķ�����������̱Ƚ����ã������ɱ�����ص�����������һ����Ҫһ����˼ά���� 


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| an |
| 2an-1 |
| 2an |
| 2an+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| a | 2 n |
| S | 2 n |
| 2 | ||
4
|
| 1 |
| 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 | ||
4
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| S | 2 n |
| 2 | ||
|
| 1 |
| 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| an |
| 1 |
| (p-1)•3qx+1 |
| lim |
| n���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com