
【题目】选修4—4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为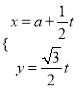
![]() .以坐标原点为极点,以
.以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于A,B两点,当
交于A,B两点,当![]() 时,求
时,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】(2017·太原市模拟题)已知a,b,c分别是△ABC的内角A,B,C所对的边,a=2bcosB,b≠c.
(1)证明:A=2B;
(2)若a2+c2=b2+2acsinC,求A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln x+ax-![]() +b.
+b.
(1)若函数g(x)=f(x)+![]() 为减函数,求实数a的取值范围;
为减函数,求实数a的取值范围;
(2)若f(x)≤0恒成立,证明:a≤1-b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)经过点(
(a>b>0)经过点(![]() ,1),以原点为圆心、椭圆短半轴长为半径的圆经过椭圆的焦点.
,1),以原点为圆心、椭圆短半轴长为半径的圆经过椭圆的焦点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点(-1,0)的直线l与椭圆C相交于A,B两点,试问在x轴上是否存在一个定点M,使得![]() 恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由.
恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共12分)
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=![]() AD=1,CD=
AD=1,CD=![]() .
.
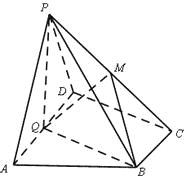
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-ax+2lnx,a∈R.
(Ⅰ)若曲线y=f(x)在(1,f(1))处的切线垂直于直线y=x,求函数f(x)的单调区间;
(Ⅱ)若x>1时,f(x)>0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地棚户区改造建筑用地平面示意图如图所示,经规划调研确定,棚改规划建筑用地区域近似为圆面,该圆面的内接四边形ABCD是原棚户区建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.
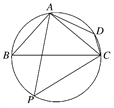
(1)请计算原棚户区建筑用地ABCD的面积及AC的长;
(2)因地理条件的限制,边界AD,DC不能变更,而边界AB,BC可以调整,为了提高棚户区建筑用地的利用率,请在![]() 上设计一点P,使得棚户区改造后的新建筑用地APCD的面积最大,并求出最大值.
上设计一点P,使得棚户区改造后的新建筑用地APCD的面积最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项竞赛分为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是![]() 且各阶段通过与否相互独立.
且各阶段通过与否相互独立.
(1)求该选手在复赛阶段被淘汰的概率;
(2)设该选手在竞赛中回答问题的个数为ξ,求ξ的分布列与均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
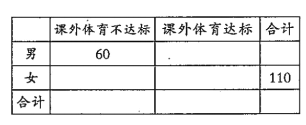
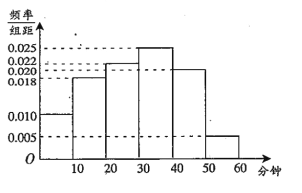
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集的数据分成![]() 六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
(1)请根据直方图中的数据填写下面的![]() 列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
(2)现按照“课外体育达标”与“课外体育不达标”进行分层抽样,抽取8人,再从这8名学生中随机抽取3人参加体育知识问卷调查,记“课外体育不达标”的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com