
【题目】某项竞赛分为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是![]() 且各阶段通过与否相互独立.
且各阶段通过与否相互独立.
(1)求该选手在复赛阶段被淘汰的概率;
(2)设该选手在竞赛中回答问题的个数为ξ,求ξ的分布列与均值.
【答案】(1) ![]() (2) ξ的分布列为:
(2) ξ的分布列为:
ξ | 1 | 2 | 3 |
P |
|
|
|
Eξ=2
【解析】试题分析:(1)选手在复赛阶段被淘汰的概率P=P(A ![]() ),分别求出P(A)=
),分别求出P(A)=![]() ,P(B)=
,P(B)= ![]() ,代入公式P=P(A
,代入公式P=P(A ![]() )=P(A)P(
)=P(A)P(![]() )得到结果。(2)根据题意得到P(ξ=1)=
)得到结果。(2)根据题意得到P(ξ=1)= ![]() ,P(ξ=2)=
,P(ξ=2)= ![]() ,P(ξ=3)=
,P(ξ=3)=![]() ,再根据期望公式得到结果。
,再根据期望公式得到结果。
解析:
(1)解:记“该选手通过初赛”为事件A,“该选手通过复赛”为事件B,“该选手通过决赛”为事件C,则P(A)=![]() ,P(B)=
,P(B)= ![]() ,P(C)=
,P(C)=![]()
那么该选手在复赛阶段被淘汰的概率P=P(A ![]() )=P(A)P(
)=P(A)P(![]() )=
)= ![]()
(2)解:ξ可能取值为1,2,3.
P(ξ=1)=1﹣![]() =
= ![]() ,
,
P(ξ=2)= ![]()
P(ξ=3)= ![]() +
+![]() =
=![]()
故ξ的分布列为:
ξ | 1 | 2 | 3 |
P |
|
|
|
Eξ=1![]()
![]() +2
+2![]()
![]() +3
+3![]()
![]() =2
=2


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,a10=4a3,a4=3a1+7.
(1)求通项公式an;
(2)若bn=an-2an+2,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为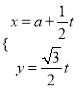
![]() .以坐标原点为极点,以
.以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于A,B两点,当
交于A,B两点,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856264)
已知函数f(x)=aln x,e为自然对数的底数.
(Ⅰ)曲线f(x)在点A(1,f(1))处的切线与坐标轴所围成的三角形的面积为2,求实数a的值;
(Ⅱ)若f(x)≥1-![]() 恒成立,求实数a的值取值范围.
恒成立,求实数a的值取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·河西五市二联)下列说法正确的是( )
A. 命题“x∈R,ex>0”的否定是“x∈R,ex>0”
B. 命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题
C. “x2+2x≥ax在x∈[1,2]上恒成立”“(x2+2x)min≥(ax)min在x∈[1,2]上恒成立”
D. 命题“若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x)万元,当年产量不足80千件时,C(x)=![]() x2+10x(万元);当年产量不少于80千件时,C(x)=51x+
x2+10x(万元);当年产量不少于80千件时,C(x)=51x+![]() -1 450(万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
-1 450(万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
(1)写出年利润L(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届吉林省普通中学高三第二次调研】某校冬令营有三名男同学A,B,C和三名女同学X,Y,Z,
(1)从6人中抽取2人参加知识竞赛,求抽取的2人都是男生的概率;
(2)若从这3名男生和3名女生中各任选一名,求这2人中包含A且不包含X的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com