
 ≤a≤1)的概率.
≤a≤1)的概率.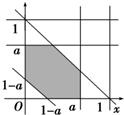 解:设第一段的长度为x,第二段的长度为y,第三段的长度为1-x-y,
解:设第一段的长度为x,第二段的长度为y,第三段的长度为1-x-y, .
. ≤a≤1)”所对应的几何区域可表示为:
≤a≤1)”所对应的几何区域可表示为: ≤a≤
≤a≤ 时,为(3a-1)2/2,
时,为(3a-1)2/2, ≤a≤1)”的概率为P=
≤a≤1)”的概率为P= =(3a-1)2;
=(3a-1)2; ≤a≤1时,为
≤a≤1时,为 -
-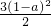 .
. ≤a≤1)”的概率为P=1-3(1-a)2.
≤a≤1)”的概率为P=1-3(1-a)2. ≤a≤1)的概率.
≤a≤1)的概率.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com