练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    将长为1 的棒任意地折成三段，求三段的长度都不超过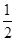的概率.

     

    【答案】

    【解析】利用几何概型概率计算公式可知，设第一段的长度为 x，第二段的长度为 y，第三段的长度为 1-x-y，则基本事件组所对应的几何区域可表示为

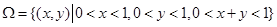    ，事件“三段的长度都不超过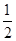”所对应的几何区域可表示为

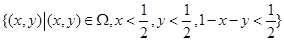    ，即图中最中间三角形区域，此区域面积：为  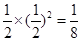 利用面积比求解概率值即可。

    解：设第一段的长度为 x，第二段的长度为 y，第三段的长度为 1-x-y，       1分

    则基本事件组所对应的几何区域可表示为

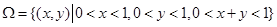    ，即图中黄色区域，此区域面积为  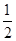 4分

    事件“三段的长度都不超过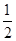”所对应的几何区域可表示为

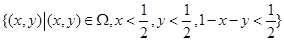    ，即图中最中间三角形区域，此区域面积：为  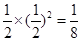                                                        10分

    此时事件“三段的长度都不超过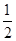的概率为                          12分

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    将长为1的棒任意地折成三段，求：三段的长度都不超过a（
    13
    ≤a≤1）的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    将长为1的棒任意地折成三段，求三段的长度都不超过的概率。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    将长为1的棒任意地折成三段，求：三段的长度都不超过a（数学公式≤a≤1）的概率．

    查看答案和解析>>

    科目：高中数学 来源：2010年福建省高考数学一轮复习：11.2 概率的应用（解析版） 题型：解答题

    将长为1的棒任意地折成三段，求：三段的长度都不超过a（≤a≤1）的概率．

    查看答案和解析>>

    同步练习册答案