
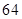 ; (2)
; (2)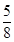 ; (3)分布列见解析,期望为
; (3)分布列见解析,期望为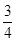 .
.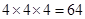 种;(2)找出三名同学中至少有二人参加同一组活动的对立面,三名同学选择三个小组的概率为
种;(2)找出三名同学中至少有二人参加同一组活动的对立面,三名同学选择三个小组的概率为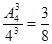 ,则可得所求概率为
,则可得所求概率为 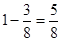 ;(3)X的可能取值为0,1,2,3,分别求出所对应的概率,列出分布列,进一步求出期望.
;(3)X的可能取值为0,1,2,3,分别求出所对应的概率,列出分布列,进一步求出期望.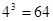 种.(4分)
种.(4分)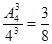 ,
,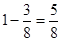 . (8分)
. (8分)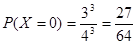 ,
,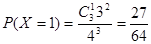 ,
,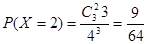 ,
,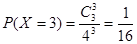 , (12分)
, (12分)| X | 0 | 1 | 2 | 3 |
| P | 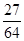 | 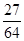 | 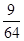 | 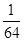 |
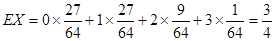 . (14分)
. (14分)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
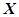 为取得红球的个数.
为取得红球的个数.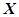 的分布列;
的分布列;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.①③ | B.②④ | C.①④ | D.都不对 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 测试 指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
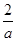 +
+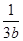 的最小值为( )
的最小值为( )A.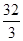 | B.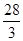 | C.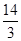 | D.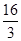 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 分,海选不合格记
分,海选不合格记 分.假设甲、乙、丙海选合格的概率分别为
分.假设甲、乙、丙海选合格的概率分别为 ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的. ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
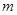 个红球和
个红球和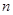 个篮球
个篮球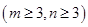 ,从乙盒中随机抽取
,从乙盒中随机抽取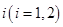 个球放入甲盒中.
个球放入甲盒中.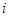 个球后,甲盒中含有红球的个数记为
个球后,甲盒中含有红球的个数记为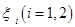 ;
;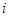 个球后,从甲盒中取1个球是红球的概率记为
个球后,从甲盒中取1个球是红球的概率记为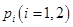 .
.A.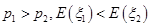 | B. |
C.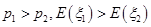 | D.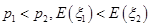 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com